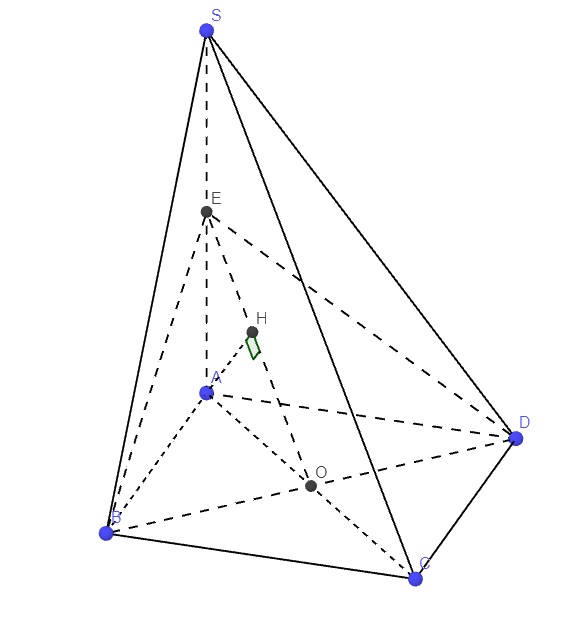
Gọi O là tâm đáy, E là trung điểm SA
\(\Rightarrow OE\) là đường trung bình tam giác SAC \(\Rightarrow OE||SC\)
\(\Rightarrow SC||\left(BDE\right)\Rightarrow d\left(SC;BD\right)=d\left(SC;\left(BDE\right)\right)=d\left(S;\left(BDE\right)\right)\)
Lại có E là trung điểm SA \(\Rightarrow\left\{{}\begin{matrix}SA\cap\left(BDE\right)=E\\SE=AE\end{matrix}\right.\)
\(\Rightarrow d\left(S;\left(BDE\right)\right)=d\left(A;\left(BDE\right)\right)\)
Trong tam giác AEO, từ A kẻ \(AH\perp OE\) (1)
\(\left\{{}\begin{matrix}BD\perp AC\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BD\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(BDE\right)\Rightarrow AH=d\left(A;\left(BDE\right)\right)\)
\(AC=AB\sqrt{2}=\sqrt{2}\Rightarrow SA=AC.tan45^0=\sqrt{2}\)
\(AE=\dfrac{1}{2}SA=\dfrac{\sqrt{2}}{2}\) ; \(OA=\dfrac{1}{2}AC=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow AH=\dfrac{AE.OA}{\sqrt{AE^2+OA^2}}=\dfrac{1}{2}\)
\(\Rightarrow d\left(SC;BD\right)=AH=\dfrac{1}{2}\)