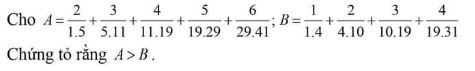\(a.A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\\ =1-\dfrac{1}{100}\\ =\dfrac{99}{100}\\ b.\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\\ =1-\dfrac{1}{101}\\ =\dfrac{100}{101}\\ c.\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)...\left(1-\dfrac{1}{2004}\right)\\ =\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2003}{2004}\\ =\dfrac{1}{2004}\\ d.5\dfrac{9}{10}:\dfrac{3}{2}-\left(2\dfrac{1}{3}\cdot4\dfrac{1}{2}-2\cdot2\dfrac{1}{3}\right):\dfrac{7}{4}\\ =\dfrac{59}{10}\cdot\dfrac{2}{3}-\left(\dfrac{7}{3}\cdot\dfrac{9}{2}-2\cdot\dfrac{7}{3}\right):\dfrac{7}{4}\\ =\dfrac{59}{15}-\dfrac{7}{3}\cdot\left(\dfrac{9}{2}-2\right)\cdot\dfrac{4}{7}\\ =\dfrac{59}{15}-\dfrac{4}{3}\cdot\dfrac{5}{2}\\ =\dfrac{59}{15}-\dfrac{10}{3}\\ =\dfrac{9}{15}=\dfrac{3}{5}\)
Bài 18:
a: \(\dfrac{3}{2}\cdot\dfrac{4}{5}-x=\dfrac{2}{3}\)
=>\(\dfrac{12}{10}-x=\dfrac{2}{3}\)
=>\(x=\dfrac{12}{10}-\dfrac{2}{3}=\dfrac{6}{5}-\dfrac{2}{3}=\dfrac{8}{15}\)
b: \(x\cdot3\dfrac{1}{3}=3\dfrac{1}{3}:4\dfrac{1}{4}\)
=>\(x\cdot\dfrac{10}{3}=\dfrac{10}{3}:\dfrac{17}{4}\)
=>\(x\cdot\dfrac{10}{3}=\dfrac{10}{3}\cdot\dfrac{4}{17}\)
=>\(x=\dfrac{4}{17}\)
c: \(5\dfrac{2}{3}:x=3\dfrac{2}{3}-2\dfrac{1}{2}\)
=>\(\dfrac{17}{3}:x=\dfrac{11}{3}-\dfrac{5}{2}=\dfrac{22}{6}-\dfrac{15}{6}=\dfrac{7}{6}\)
=>\(x=\dfrac{17}{3}:\dfrac{7}{6}=\dfrac{17}{3}\cdot\dfrac{6}{7}=\dfrac{17\cdot2}{7}=\dfrac{34}{7}\)
Bài 19:
a: \(A=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}=\dfrac{99}{100}\)
b: \(B=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\)
\(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(=1-\dfrac{1}{101}=\dfrac{100}{101}\)
c: \(C=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{2003}\right)\cdot\left(1-\dfrac{1}{2004}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{2002}{2003}\cdot\dfrac{2003}{2004}=\dfrac{1}{2004}\)
d: \(D=5\dfrac{9}{10}:\dfrac{3}{2}-\left(2\dfrac{1}{3}\cdot4\dfrac{1}{2}-2\cdot2\dfrac{1}{3}\right):\dfrac{7}{4}\)
\(=\dfrac{59}{10}\cdot\dfrac{2}{3}-\left(\dfrac{7}{3}\cdot\dfrac{9}{2}-2\cdot\dfrac{7}{3}\right)\cdot\dfrac{4}{7}\)
\(=\dfrac{59}{15}-\dfrac{7}{3}\cdot\dfrac{5}{2}\cdot\dfrac{4}{7}=\dfrac{59}{15}-\dfrac{10}{3}=\dfrac{59}{15}-\dfrac{50}{15}=\dfrac{9}{15}=\dfrac{3}{5}\)
\(a,\dfrac{3}{2}.\dfrac{4}{5}-x=\dfrac{2}{3}\)
\(=>\dfrac{6}{5}-x=\dfrac{2}{3}\)
\(=>x=\dfrac{8}{15}\)
\(b,x.3\dfrac{1}{3}=3\dfrac{1}{3}:4\dfrac{1}{4}\)
\(=>x.\dfrac{10}{3}=\dfrac{10}{3}:\dfrac{17}{4}\)
\(=>x=\dfrac{4}{17}\)
\(c,5\dfrac{2}{3}:x=3\dfrac{2}{3}-2\dfrac{1}{2}\)
\(=>\dfrac{17}{3}:x=\dfrac{7}{6}\)
\(=>x=\dfrac{34}{7}\)
`B19:`
\(a,A=\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\)
\(=>A=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=>A=1-\dfrac{1}{100}=\dfrac{99}{100}\)
\(b,B=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{99.101}\)
\(=>B=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\)
\(=>B=1-\dfrac{1}{101}=\dfrac{100}{101}\)
\(c,C=\left(1-\dfrac{1}{2}\right).\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{4}\right).....\left(1-\dfrac{1}{2023}\right)\left(1-\dfrac{1}{2024}\right)\)
\(=>C=\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.....\dfrac{2022}{2023}.\dfrac{2023}{2024}\)
\(=>C=\dfrac{1}{2024}\)
\(d,D=5\dfrac{9}{10}:\dfrac{3}{2}-\left(2\dfrac{1}{3}.4\dfrac{1}{2}-2.2\dfrac{1}{3}\right):\dfrac{7}{4}\)
\(=>D=\dfrac{59}{15}-\left(\dfrac{21}{2}-\dfrac{14}{3}\right):\dfrac{7}{4}\)
\(=>D=\dfrac{59}{15}-\dfrac{35}{6}:\dfrac{7}{4}\)
\(=>D=\dfrac{59}{15}-\dfrac{10}{3}=\dfrac{3}{5}\)

















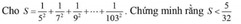

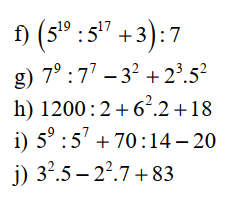 giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim