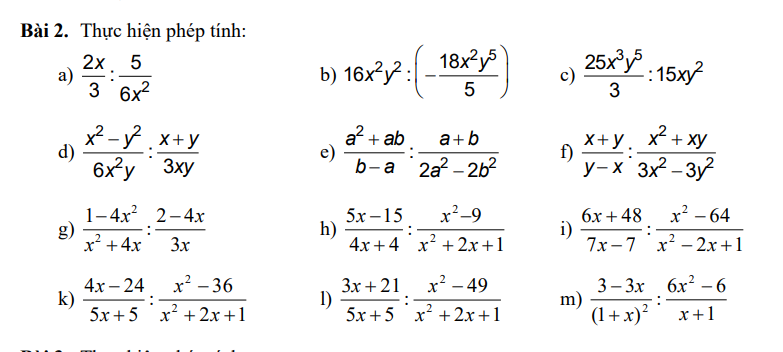Question

làm giúp em bài 12 với ạ.​

Answer 1

Câu 12:

a: Xét ΔCHA vuông tại H và ΔCAD vuông tại A có

\(\widehat{HCA}\) chung

Do đó: ΔCHA~ΔCAD
=>\(\dfrac{CH}{CA}=\dfrac{CA}{CD}\)

=>\(CA^2=CH\cdot CD\)

Ta có: AH\(\perp\)DC

AB//CD

Do đó: HA\(\perp\)AB

=>ΔBAI vuông tại A

Ta có AC\(\perp\)AD

AD//BC

Do đó: AC\(\perp\)BC tại C

Xét ΔACB vuông tại C và ΔAIC vuông tại C có

\(\widehat{ACB}=\widehat{AIC}\left(=90^0-\widehat{IAC}\right)\)

Do đó: ΔACB~ΔAIC

=>\(\dfrac{AC}{CI}=\dfrac{CB}{AC}\)

=>\(AC^2=CI\cdot CB=CH\cdot CD\)

b: Xét ΔAHC vuông tại H và ΔACI vuông tại C có

\(\widehat{HAC}\) chung

Do đó: ΔAHC~ΔACI

=>\(\dfrac{AH}{AC}=\dfrac{AC}{AI}\)

=>\(AH\cdot AI=AC^2\)

Xét ΔDHA vuông tại H và ΔDAC vuông tại A có

\(\widehat{HDA}\) chung

Do đó: ΔDHA~ΔDAC

=>\(\dfrac{DH}{DA}=\dfrac{DA}{DC}\)

=>\(DH\cdot DC=DA^2\)

Xét ΔBCA vuông tại C và ΔBAI vuông tại A có

\(\widehat{CBA}\) chung

Do đó: ΔBCA~ΔBAI

=>\(\dfrac{BC}{BA}=\dfrac{BA}{BI}\)

=>\(BC\cdot BI=BA^2=DC^2\)

\(AH\cdot AI+DH\cdot DC=AC^2+DA^2=DC^2\)

\(=BC\cdot BI\)