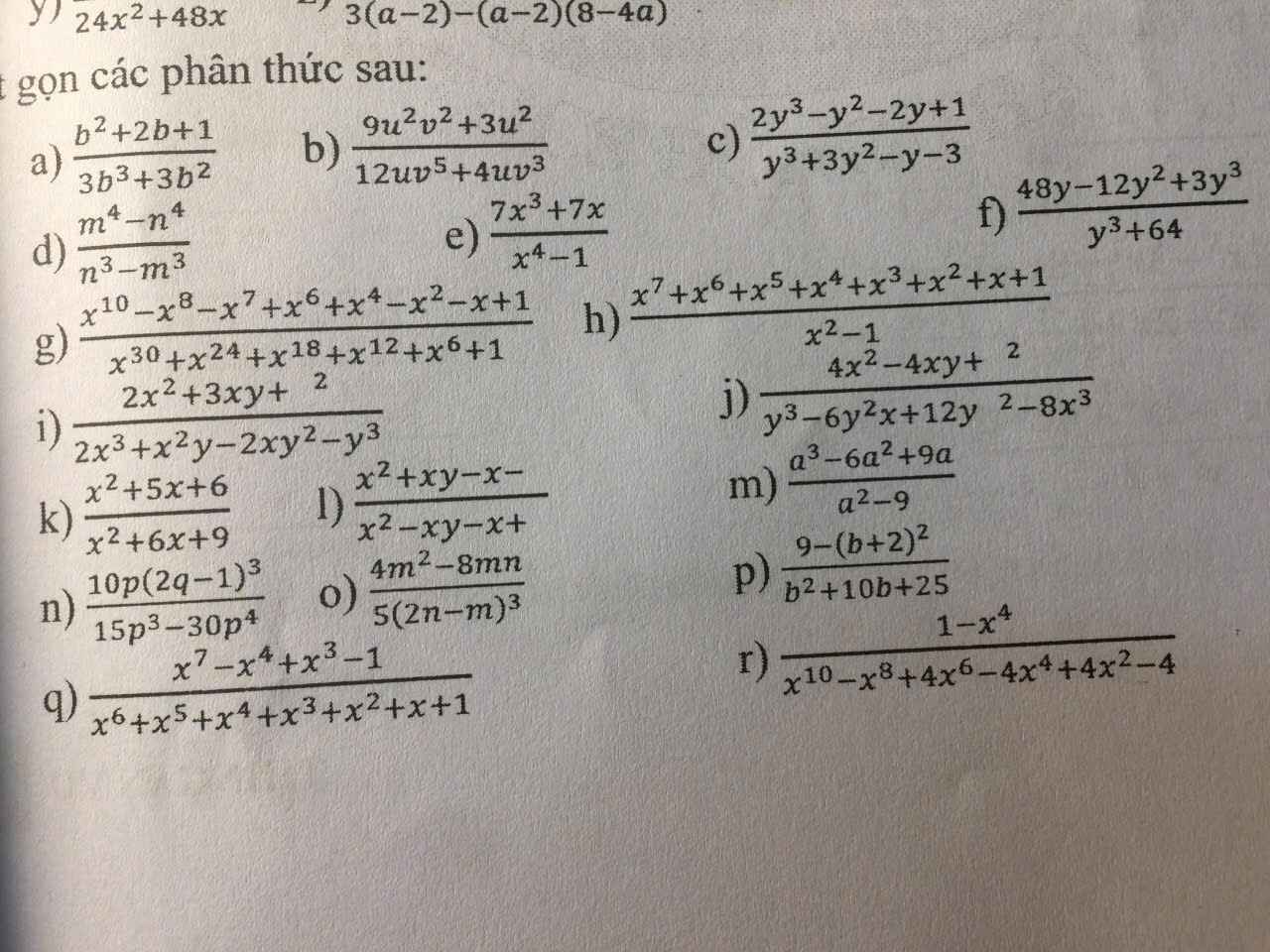a: \(\dfrac{b^2+2b+1}{3b^3+3b^2}=\dfrac{\left(b+1\right)^2}{3b^2\left(b+1\right)}=\dfrac{1}{3b^2}\)
b: \(\dfrac{9u^2v^2+3u^2}{12uv^5+4uv^3}\)
\(=\dfrac{3u^2\left(3v^2+1\right)}{4uv^3\left(3v^2+1\right)}=\dfrac{3y}{4v^3}\)
c: \(\dfrac{2y^3-y^2-2y+1}{y^3+3y^2-y-3}\)
\(=\dfrac{y^2\left(2y-1\right)-\left(2y-1\right)}{y^2\left(y+3\right)-\left(y+3\right)}\)
\(=\dfrac{\left(2y-1\right)\left(y^2-1\right)}{\left(y+3\right)\left(y^2-1\right)}=\dfrac{2y-1}{y+3}\)
d: \(\dfrac{m^4-n^4}{n^3-m^3}\)
\(=\dfrac{\left(m^2-n^2\right)\left(m^2+n^2\right)}{\left(n-m\right)\left(n^2+nm+m^2\right)}\)
\(=\dfrac{\left(m-n\right)\left(m+n\right)\left(m^2+n^2\right)}{-\left(m-n\right)\left(m^2+mn+n^2\right)}\)
\(=\dfrac{-\left(m+n\right)\left(m^2+n^2\right)}{m^2+mn+n^2}\)
e: \(\dfrac{7x^3+7x}{x^4-1}=\dfrac{7x\left(x^2+1\right)}{\left(x^2+1\right)\left(x^2-1\right)}=\dfrac{7x}{x^2-1}\)
f: \(\dfrac{48y-12y^2+3y^3}{y^3+64}\)
\(=\dfrac{3y\left(y^2-4y+16\right)}{\left(y+4\right)\left(y^2-4y+16\right)}\)
\(=\dfrac{3y}{y+4}\)
h: \(\dfrac{x^7+x^6+x^5+x^4+x^3+x^2+x+1}{x^2-1}\)
\(=\dfrac{x^6\left(x+1\right)+x^4\left(x+1\right)+x^2\left(x+1\right)+\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x+1\right)\left(x^6+x^4+x^2+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x^6+x^4+x^2+1}{x-1}\)
j: \(\dfrac{4x^2-4xy+y^2}{y^3-6y^2x+12yx^2-8x^3}\)
\(=\dfrac{\left(2x-y\right)^2}{\left(y-2x\right)^3}=\dfrac{1}{y-2x}\)
k: \(\dfrac{x^2+5x+6}{x^2+6x+9}=\dfrac{\left(x+3\right)\left(x+2\right)}{\left(x+3\right)^2}=\dfrac{x+2}{x+3}\)
m: \(\dfrac{a^3-6a^2+9a}{a^2-9}=\dfrac{a\left(a^2-6a+9\right)}{\left(a-3\right)\left(a+3\right)}\)
\(=\dfrac{a\left(a-3\right)^2}{\left(a-3\right)\left(a+3\right)}=\dfrac{a\left(a-3\right)}{a+3}\)
o: \(\dfrac{4m^2-8mn}{5\left(2n-m\right)^3}=\dfrac{4m\cdot m-4m\cdot2n}{5\left(2n-m\right)^3}=\dfrac{4m\left(m-2n\right)}{5\left(-m+2n\right)^3}\)
\(=\dfrac{-4m\left(m-2n\right)}{5\left(m-2n\right)^3}=\dfrac{-4m}{5\left(m-2n\right)^2}\)
n: \(\dfrac{10p\left(2q-1\right)^3}{15p^3-30p^4}\)
\(=\dfrac{10p\left(2q-1\right)^3}{15p^3\left(1-2p\right)}=\dfrac{2}{3p^2}\cdot\dfrac{\left(2q-1\right)^3}{1-2p}\)
p: \(\dfrac{9-\left(b+2\right)^2}{b^2+10b+25}\)
\(=\dfrac{\left(3-b-2\right)\left(3+b+2\right)}{\left(b+5\right)^2}\)
\(=\dfrac{\left(1-b\right)\left(b+5\right)}{\left(b+5\right)^2}=\dfrac{1-b}{b+5}\)
r: \(\dfrac{1-x^4}{x^{10}-x^8+4x^6-4x^4+4x^2-4}\)
\(=\dfrac{\left(1-x^2\right)\left(1+x^2\right)}{x^8\left(x^2-1\right)+4x^4\left(x^2-1\right)+4\left(x^2-1\right)}\)
\(=\dfrac{\left(1-x^2\right)\left(1+x^2\right)}{\left(x^2-1\right)\left(x^8+4x^4+4\right)}\)
\(=\dfrac{-\left(1+x^2\right)}{\left(x^4+2\right)^2}\)