b: \(A=\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{2-\sqrt{x}}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}+2+\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+2+x-9-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{1}{\sqrt{x}-2}\)
c:
ĐKXĐ của M là \(\left\{{}\begin{matrix}x>=0\\x\notin\left\{1;9;4\right\}\end{matrix}\right.\)
\(M=A:B\)
\(=\dfrac{1}{\sqrt{x}-1}:\dfrac{1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
Để M>2 thì M-2>0
=>\(\dfrac{\sqrt{x}-2-2\left(\sqrt{x}-1\right)}{\sqrt{x}-1}>0\)
=>\(\dfrac{-\sqrt{x}}{\sqrt{x}-1}>0\)
mà \(-\sqrt{x}< =0\)
nên \(\sqrt{x}-1< 0\)
=>\(\sqrt{x}< 1\)
=>0<=x<1
d: Để M là số nguyên thì \(\sqrt{x}-2⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1-1⋮\sqrt{x}-1\)
=>\(-1⋮\sqrt[]{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{2;0\right\}\)
=>\(x\in\left\{4;0\right\}\)
Kết hợp ĐKXĐ của M, ta được: x=0

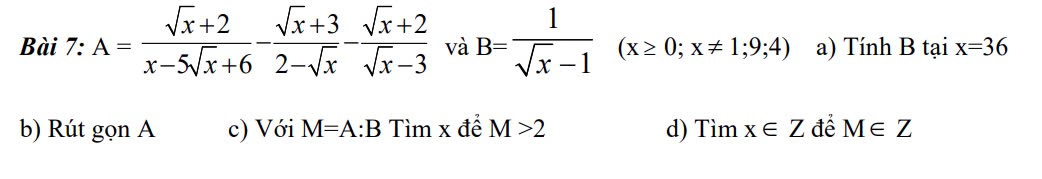




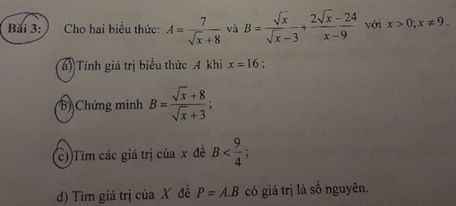


 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
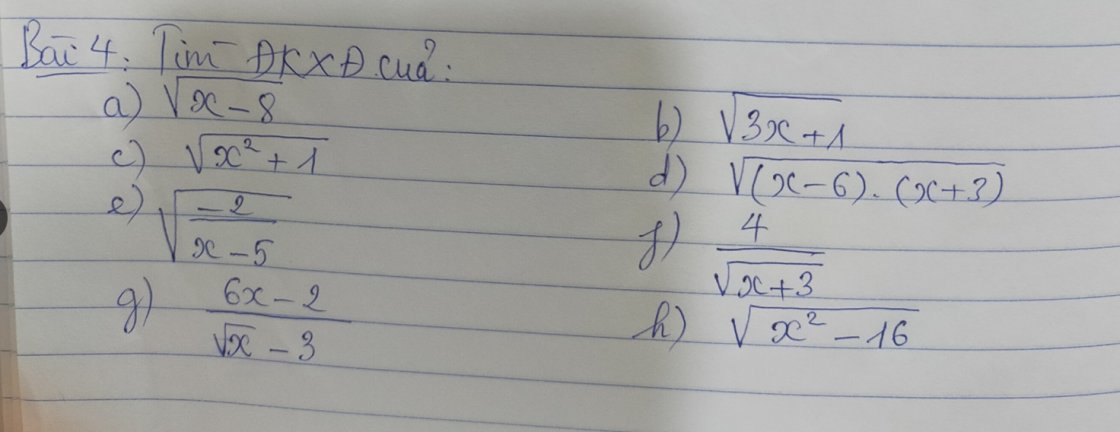











 không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
 vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á