Chọn C
Hình bát diện đều có 8 mặt, mỗi mặt là tam giác đều, có 6 đỉnh và 12 cạnh.
Chọn C
Hình bát diện đều có 8 mặt, mỗi mặt là tam giác đều, có 6 đỉnh và 12 cạnh.
Kí hiệu M là số mặt, Đ là số đỉnh và C là số cạnh của một hình bát diện đều. Khi đó bộ (M, Đ, C) tương ứng với bộ số nào?
A. (M, Đ, C) = (6,12,8)
B. (M, Đ, C) = (8,6,12)
C. (M, Đ, C) = (12,8,6)
D. (M, Đ, C) = (8,12,6)
Gọi M, C, Đ thứ tự là số mặt, số cạnh, số đỉnh của hình bát diện đều. Khi đó S=M+C+Đ bằng:
A. S=24
B. S=26
C. S=30
D. S=14
Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng?
A. N ¯ > 4 , M > 4 , C > 6
B. N ¯ > 5 , M > 5 , C > 7
C. N ¯ ≥ 4 , M ≥ 4 , C ≥ 6
D. N ¯ ≥ 5 , M ≥ 5 , C ≥ 7
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình đa diện (H) có các mặt là nhứng tam giác, mỗi đỉnh là đỉnh chung của đúng 3 mặt. Gọi số các đỉnh, cạnh, mặt của hình đa diện (H) lần lượt là d, c, m. Khi đó:
A. d > m
B. d < m
C. d = m
D. d + m = c
Một hình đa diện có các mặt là các tam giác có số mặt M và số cạnh C của đa diện đó thỏa mãn hệ thức nào dưới đây
A. 3C=2M
B. C=2M
C. 3M=2C
D. 2C=M
Một hình đa diện có các mặt là các tam giác thì số mặt M và số cạnh C của đa diện đó thỏa mãn hệ thức nào dưới đây
A. 3C=2M
B. C=2M
C. 3M=2C
D. 2C=M
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A (-1; 0) và C ( m ; m ) , với m > 0. Biết rằng đồ thị hàm số y= x chia hình (H) thành hai phần có diện tích bằng nhau, tìm m .
![]()
![]()
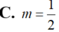
![]()
Trong mặt phẳng tọa độ, cho hình chữ nhật (H) có một cạnh nằm trên trục hoành, và có hai đỉnh trên một đường chéo là A(-1;0) và C ( m ; m ) , với m>0. Biết rằng đồ thị hàm số y = x chia hình (H) thành hai phần có diện tích bằng nhau, tìm m
![]()
![]()
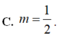
![]()
Hình bát diện đều có số đỉnh, số cạnh, số mặt tương ứng là:
A. 12; 8; 6
B. 12; 6; 8
C. 6; 12; 8
D. 8; 6; 12