Các câu hỏi tương tự
Một hình đa diện có các mặt là các tam giác thì số mặt M và số cạnh C của đa diện đó thỏa mãn hệ thức nào dưới đây
A. 3C=2M
B. C=2M
C. 3M=2C
D. 2C=M
Trong các mệnh đề sau, mệnh đề nào đúng?Cho hình đa diện (H) có các mặt là nhứng tam giác, mỗi đỉnh là đỉnh chung của đúng 3 mặt. Gọi số các đỉnh, cạnh, mặt của hình đa diện (H) lần lượt là d, c, m. Khi đó: A. d m B. d m C. d m D. d + m c
Đọc tiếp
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình đa diện (H) có các mặt là nhứng tam giác, mỗi đỉnh là đỉnh chung của đúng 3 mặt. Gọi số các đỉnh, cạnh, mặt của hình đa diện (H) lần lượt là d, c, m. Khi đó:
A. d > m
B. d < m
C. d = m
D. d + m = c
Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng? A.
N
¯
4
,
M
4
,
C
6
B.
N
¯...
Đọc tiếp
Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng?
A. N ¯ > 4 , M > 4 , C > 6
B. N ¯ > 5 , M > 5 , C > 7
C. N ¯ ≥ 4 , M ≥ 4 , C ≥ 6
D. N ¯ ≥ 5 , M ≥ 5 , C ≥ 7
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây? A.
x
2
+
2
x
y
−
y
2
160
B.
x...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N, P lần lượt là trung điểm của các cạnh SD, CD, BC. Thể tích khối chóp S.ABPN là x, thể tích khối tứ diện CMNP là y. Giá trị của x,y thỏa mãn các bất đẳng thức nào dưới đây?
A. x 2 + 2 x y − y 2 > 160
B. x 2 − 2 x y + 2 y 2 < 109
C. x 2 + x y − y 4 < 145
D. x 2 − x y + y 4 > 125
Hình đa diện đều nào dưới đây có tất cả các mặt không là tam giác đều A. Bát giác đều B. Hình 20 mặt đều C. Hình 12 mặt đều D. Tứ diện đều
Đọc tiếp
Hình đa diện đều nào dưới đây có tất cả các mặt không là tam giác đều
A. Bát giác đều
B. Hình 20 mặt đều
C. Hình 12 mặt đều
D. Tứ diện đều
Hình đa diện đều nào dưới đây có tất cả các mặt không phải là tam giác đều? A. Bát diện đều B. Hình 20 mặt đều C. Hình 12 mặt đều D. Tứ diện đều.
Đọc tiếp
Hình đa diện đều nào dưới đây có tất cả các mặt không phải là tam giác đều?
A. Bát diện đều
B. Hình 20 mặt đều
C. Hình 12 mặt đều
D. Tứ diện đều.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
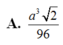
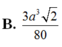
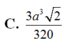
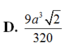
Cho đa diện (H), biết rằng mỗi mặt của (H) đều là những đa giác có số cạnh là lẻ và tồn tại ít nhất một mặt có số cạnh khác với các mặt còn lại. Hỏi khẳng định nào đúng trong các khẳng định sau A. Tổng số các cạnh của (H) bằng 9. B. Tổng số các cạnh của (H) bằng 5. C. Tổng số các cạnh của (H) là số lẻ. C. Tổng số các cạnh của (H) là số lẻ. D. Tổng số các cạnh của (H) là số chẵn.
Đọc tiếp
Cho đa diện (H), biết rằng mỗi mặt của (H) đều là những đa giác có số cạnh là lẻ và tồn tại ít nhất một mặt có số cạnh khác với các mặt còn lại. Hỏi khẳng định nào đúng trong các khẳng định sau
A. Tổng số các cạnh của (H) bằng 9.
B. Tổng số các cạnh của (H) bằng 5.
C. Tổng số các cạnh của (H) là số lẻ.
C. Tổng số các cạnh của (H) là số lẻ.
D. Tổng số các cạnh của (H) là số chẵn.
Mỗi cạnh của một hình đa diện là cạnh chung của đúng n mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Mỗi cạnh của một hình đa diện là cạnh chung của đúng n mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
![]()
![]()
![]()