Câu 1: Ta có: \(25>24\Leftrightarrow\sqrt{25}>\sqrt{24}\Leftrightarrow5>2\sqrt{6}\)
Vậy: \(5>2\sqrt{6}\)
Câu 2:
\(\sqrt{x^2}=5\)
\(\Leftrightarrow\left|x\right|=5\)
\(\Leftrightarrow x=5\) hoặc \(x=-5\)
Vậy \(x=5\) hoặc \(x=-5\)
Câu 3:
\(A=\sqrt{4x-4}+2\sqrt{x-1}-\sqrt{9x-9}\)
\(=\sqrt{4\left(x-1\right)}+2\sqrt{x-1}-\sqrt{9\left(x-1\right)}\)
\(=2\sqrt{x-1}+2\sqrt{x-1}-3\sqrt{x-1}\)
\(=\left(2+2-3\right)\sqrt{x-1}\)
\(=\sqrt{x-1}\)
Câu 4: Điều kiện: \(3-2x\ge0\Leftrightarrow2x\le3\Leftrightarrow x\le\dfrac{3}{2}\)
Câu 5:
\(\dfrac{\sqrt{7}+\sqrt{5}}{\sqrt{7}-\sqrt{5}}+\dfrac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}\)
\(=\dfrac{\left(\sqrt{7}+\sqrt{5}\right)^2+\left(\sqrt{7}-\sqrt{5}\right)^2}{\left(\sqrt{7}-\sqrt{5}\right)\left(\sqrt{7}+\sqrt{5}\right)}\)
\(=\dfrac{7+2\sqrt{35}+5+7-2\sqrt{35}+5}{7-5}\)
\(=\dfrac{24}{2}\)
\(=12\)
Câu 6:
\(M=\left(\dfrac{3}{\sqrt{1+a}}+\sqrt{1-a}\right):\left(\dfrac{3}{\sqrt{1-a^2}}+1\right)\)
\(=\dfrac{3+\sqrt{1-a}.\sqrt{1+a}}{\sqrt{1+a}}:\dfrac{3+\sqrt{1-a^2}}{\sqrt{1-a^2}}\)
\(=\dfrac{3+\sqrt{1-a}.\sqrt{1+a}}{\sqrt{1+a}}:\dfrac{3+\sqrt{1-a}.\sqrt{1+a}}{\sqrt{1-a}.\sqrt{1+a}}\)
\(=\dfrac{3+\sqrt{1-a}.\sqrt{1+a}}{\sqrt{1+a}}.\dfrac{\sqrt{1-a}.\sqrt{1+a}}{3+\sqrt{1-a}.\sqrt{1+a}}\)
\(=\sqrt{1-a}\)
Câu 7:
Ta có: \(\sqrt{x+2019}\ge0\)
\(\Leftrightarrow\sqrt{x+2019}+\sqrt{2019}\ge\sqrt{2019}\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x+2019}+\sqrt{2019}}\le\dfrac{1}{\sqrt{2019}}\)
\(\Leftrightarrow\dfrac{\sqrt{2019}}{\sqrt{x+2019}+\sqrt{2019}}\le\dfrac{\sqrt{2019}}{\sqrt{2019}}\)
\(\Leftrightarrow A\le1\)
Đẳng thức xảy ra \(\Leftrightarrow x+2019=0\Leftrightarrow x=-2019\)
Vậy \(MaxA=1\Leftrightarrow x=-2019\)
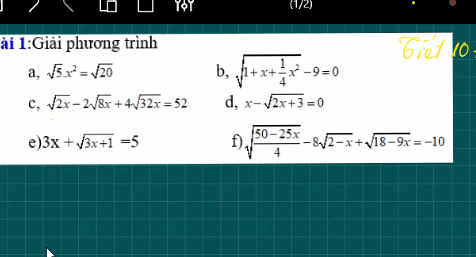
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
