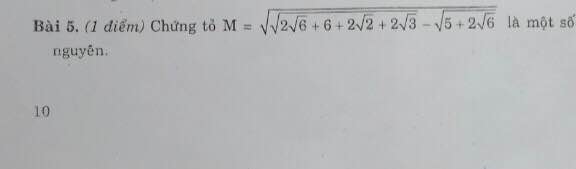1.
\(2\sqrt{6}=2\sqrt{\dfrac{24}{4}}< 2\sqrt{\dfrac{25}{4}}=5\)
Vậy \(2\sqrt{6}< 5\)
2.
\(\sqrt{x^2}=5\Leftrightarrow\left|x\right|=5\Rightarrow\left[{}\begin{matrix}x=5\\x=-5\end{matrix}\right.\)
3.
\(A=\sqrt{4x-4}+2\sqrt{x-1}-\sqrt{9x-9}=\sqrt{4\left(x-1\right)}+2\sqrt{x-1}-\sqrt{9\left(x-1\right)}\)
\(=2\sqrt{x-1}+2\sqrt{x-1}-3\sqrt{x-1}=4\sqrt{x-1}-3\sqrt{x-1}\)
\(=\sqrt{x-1}\)
4.
ĐKXĐ: \(3-2x\ge0\Rightarrow2x\le3\Rightarrow x\le\dfrac{3}{2}\)
5.
\(\dfrac{\sqrt{7}+\sqrt{5}}{\sqrt{7}-\sqrt{5}}+\dfrac{\sqrt{7}-\sqrt{5}}{\sqrt{7}+\sqrt{5}}=\dfrac{\left(\sqrt{7}+\sqrt{5}\right)^2+\left(\sqrt{7}-\sqrt{5}\right)^2}{\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)}\)
\(=\dfrac{12+2\sqrt{35}+12-2\sqrt{35}}{7-5}=\dfrac{24}{2}=12\)
6.
\(M=\left|\dfrac{3}{\sqrt{1+a}}+\sqrt{1-a}\right|:\left|\dfrac{3}{\sqrt{1-a^2}}+1\right|\)
\(=\left|\dfrac{3+\sqrt{1-a^2}}{\sqrt{1+a}}\right|:\left|\dfrac{3+\sqrt{1-a^2}}{\sqrt{1-a^2}}\right|\)
\(=\left|\dfrac{3+\sqrt{1-a^2}}{\sqrt{1+a}}\right|.\left|\dfrac{\sqrt{\left(1-a\right)\left(1+a\right)}}{3+\sqrt{1-a^2}}\right|\)
\(=\sqrt{1-a}\)
7.
Do \(\sqrt{x+2019}\ge0;\) \(\forall x\ge-2019\Rightarrow\sqrt{x+2019}+\sqrt{2019}\ge\sqrt{2019}\)
\(\Rightarrow\dfrac{\sqrt{2019}}{\sqrt{x+2019}+\sqrt{2019}}\le\dfrac{\sqrt{2019}}{\sqrt{2019}}=1\)
Vậy \(A_{max}=1\) khi \(x+2019=0\Rightarrow x=-2019\)