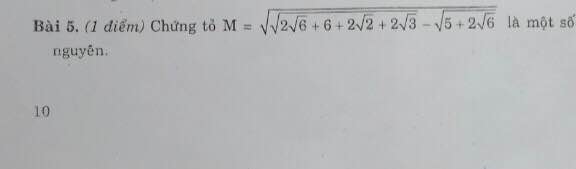Ta có: \(\sqrt{5+2\sqrt{6}}=\sqrt{\left(\sqrt{3}\right)^2+2.\sqrt{3}.\sqrt{2}.\left(\sqrt{2}\right)^2}=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\sqrt{3}+\sqrt{2}\)
Lại có: \(\sqrt{2\sqrt{6}+6+2\sqrt{2}+2\sqrt{3}}\)
\(=\sqrt{1^2+\left(\sqrt{2}\right)^2+\left(\sqrt{3}\right)^2+2.\sqrt{2}.1+2.\sqrt{3}.1+2.\sqrt{2}.\sqrt{3}}\)
\(=\sqrt{\left(1+\sqrt{2}+\sqrt{3}\right)^2}=1+\sqrt{2}+\sqrt{3}\)
Thế vào đề: \(\Rightarrow M=\sqrt{1+\sqrt{2}+\sqrt{3}-\sqrt{2}-\sqrt{3}}=1\)