Vì |3x-4y-2|2021≥0
(x-2y)2020≥0
⇒|3x-4y-2|2021+(x-2y)2020≥0
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}3x-4y-2=0\\x-2y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3.2y-4y-2=0\\x=2y\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}6y-4y=2\\x=2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2y=2\\x=2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
\(P=\left(\dfrac{x}{2}\right)^{2020}+y^{2021}=\left(\dfrac{2}{2}\right)^{2020}+y^{2021}=1^{2020}+1^{2021}=1+1=2\)


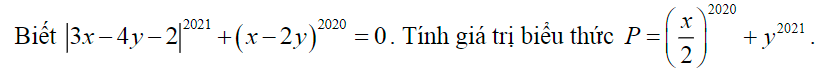




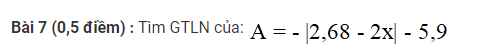

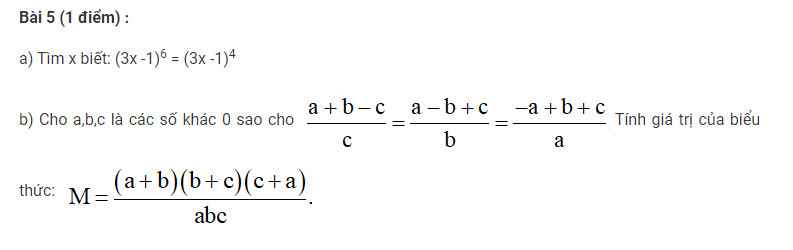 giải hộ bài này với ạ
giải hộ bài này với ạ