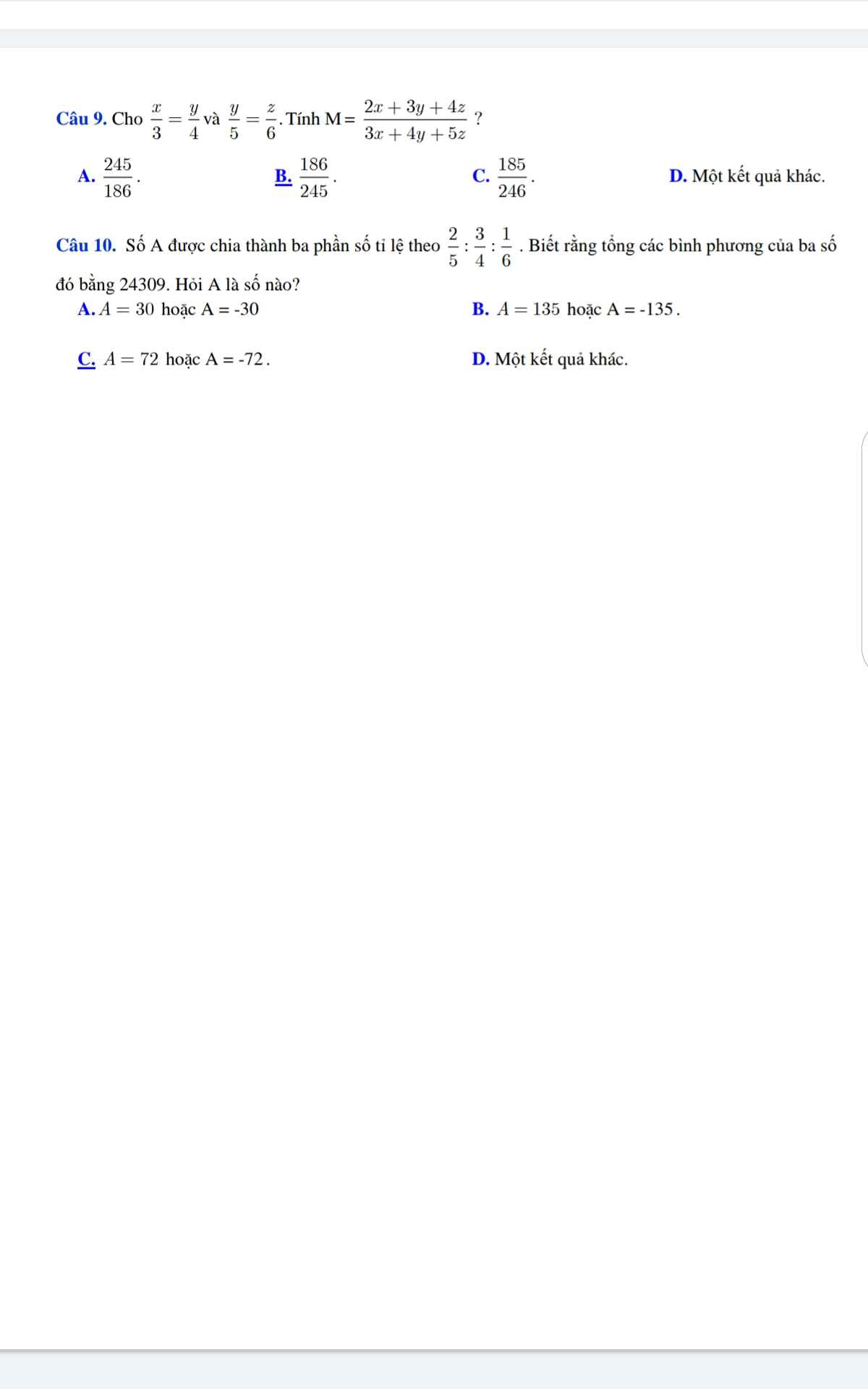
\(a,\left\{{}\begin{matrix}AC=AD\\\widehat{ACE}=\widehat{DCE}\left(CE.là.p/g\right)\\CE.chung\end{matrix}\right.\Rightarrow\Delta ACE=\Delta DCE\left(c.g.c\right)\\ \Rightarrow AE=ED\\ b,\Delta ACE=\Delta DCE\Rightarrow\widehat{BAC}=\widehat{CED}=90^0\\ \Rightarrow BC\perp DE\\ \Rightarrow\widehat{BED}+\widehat{B}=90^0\)
Mà \(\widehat{ACB}+\widehat{B}=90^0\left(\Delta ABC\perp A\right)\)
Vậy \(\widehat{BED}=\widehat{ACB}\)
\(c,\) Gọi giao của phân giác \(\widehat{BED}\) và BC là F
\(\Rightarrow\widehat{FED}=\dfrac{1}{2}\widehat{BED}\)
Lại có \(\Delta ACE=\Delta DCE\Rightarrow\widehat{AEC}=\widehat{CED}\)
Mà \(\widehat{AEC}+\widehat{CED}=\widehat{AED}\Rightarrow\widehat{CED}=\dfrac{1}{2}\widehat{AED}\)
Ta có \(\widehat{CEF}=\widehat{CED}+\widehat{FED}=\dfrac{1}{2}\left(\widehat{AED}+\widehat{DEB}\right)\)
Mà \(\widehat{AED}+\widehat{DEB}=180^0\)
Do đó \(\widehat{CEF}=90^0\Rightarrow CE\perp EF\)
Suy ra cái đề