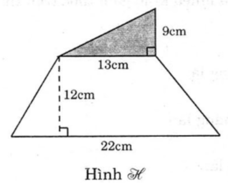
Diện tích hình tam giác là :
13 . 9 : 2 = 58,5 ( cm2 )
Diện tích hình thang là :
( 13 + 22 ) : 2 . 12 = 210 ( cm2 )
Diện tích hình " H " là :
58,5 + 210 = 268,5
ĐS :...
Tick nha
Dien h hinh tam giac la
13x9:2=58,5(cm2)
Dien h hinh thang la
(13+22:2x12=210(cm2)
Dien tinh hinh h la
58,5+210/268,5(cm2)
Ds:268,5cm2
Cm2 nay la xang ti met vuong nha may ban
Nho k cho minh nha
Diện tích tam giác là :
13* 9 : 2 = 58,5 (cm2)
Diện tích hình thang là :
( 13 + 22) : * 12= 210 (cm2)
Diện tích hình H là :
58,5 + 210 = 268,5 (cm2)
ĐS : 268 cm2
* là dấu nhân nha, chúc bạn học tốt ^^
Diện tích của hình tam giác là :
13 x 9 : 2 = 58,5 ( cm2 )
Diện tích hình thang là :
( 13 + 23 ) x 12 : 2 = 210 ( cm2)
Diện tích hình H là :
58,5 + 210 = 268,5 ( cm2)
Đáp số 268,5 cm2
k cho tui đuy. Thanks
Cho hình thang ABCD, AE = EB, DF = FC (như hình vẽ):
A B C D E F
Câu dưới đây đúng hay sai?
| Đúng | Sai | |
|---|---|---|
| Diện tích hình thang AECD bằng diện tích hình thang EBCD. | ||
| Diện tích hình thang EBCD bằng một nửa diện tích hình thang ABCD. | ||
| Diện tích hình thang AEFD bằng một nửa diện tích hình thang ABCD. |
Lưu ý: Kết quả luyện tập sẽ được lưu khi bạn hoàn thành bài học này!
00 : 11
Hoàn thành
Luyện tập lại
Diện tích hình tam giác là :
13 . 9 : 2 = 58,5 ( cm2 )
Diện tích hình thang là :
( 13 + 22 ) : 2 . 12 = 210 ( cm2 )
Diện tích hình " H " là :
58,5 + 210 = 268,5
Đáp số: 268, 5
Đúng nha