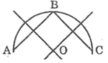
Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực cắt nhau tại O.
OA, OB, OC chính là bán kính của đường viền.
Cho đường tròn (O) và điểm A nằm bên ngoài đường tròn. Vẽ tiếp tuyến AM và cát tuyến ACD. Gọi I là trung điểm của CD. Đường tròn đường kính OA cắt (O) tại N.
a) Chứng minh tứ giác AMOI nội tiếp được một đường tròn. Xác định tâm K của đường tròn ngoại tiếp đó
b) Vẽ dây CB vuông góc với MO cắt MN tại F. Chứng minh rằng tứ giác CFIN là tứ giác nội tiếp
Cho đường tròn (O) có bán kính R = 2a và điểm A nằm ngoài đường tròn (O). Kẻ đến (O) hai tiếp tuyến AM và AN (với M, N là các tiếp điểm)
a) Chứng minh bốn điểm A,M,N,O cùng thuộc một đường tròn (C). Xác định tâm và bán kính của đường tròn (C).
b) Tính diện tích S của tứ giác AMON theo a, biết OA = 3a
c) Gọi M' là điểm đối xứng của M qua O và P là giao điểm của AO vào (O), P nằm ngoài đoạn OA. Tính sin góc MPN
Trong một hình thang câm có 2 đường tròn tiếp xúc ngoài nhau và mỗi đường tròn tiếp xúc với 2 cạnh bên và tiếp xúc với 1 đáy của hình thang. Biết bán kính của các đường tròn là 2cm và 8cm. Tính diện tích hình thang
Từ một điểm M cố định ở bên ngoài đường tròn (O), kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó. Cho MT = 20cm ,MB = 50cm,tính bán kính đường tròn
Một chiếc bàn tròn có đường kính 1m. Người ta muốn may 1 khăn trải bàn hình tròn sao cho khăn rủ xuống cách mép bàn 30cm.
Tính diện tích của khăn? Cần 1 dây đăng - ten dài bao nhiu để viền chiếc khăn trải bàn đó?
Cho đường tròn tâm O đường kính BC, A là một điểm thuộc đường tròn. H là hình chiếu của A trên BC. Vẽ đường tròn (I) có đường kính AH, cắt AB và AC theo thứ tự ở M và N.
a) Chứng minh rằng OA vuông góc với MN.
b) Vẽ đường kính AOK của đường tròn (O). Gọi E là trung điểm của HK. Chứng minh rằng E là tâm của đường tròn ngoại tiếp tứ giác BMNC.
c) Cho BC cố định. Xác định vị trí của điểm A để bán kính của đường tròn ngoại tiếp tứ giác BMNC lớn nhất.
Từ điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB và một cát tuyến MDE với đường tròn (tâm O nằm ngoài góc AME). a) Chứng minh tứ giác MAOB nội tiếp, xác định tâm và bán kính đường tròn này. b) Vẽ đường kính AK của đường tròn (O). Chứng minh BK // OM. c) DK cắt OM tại I. Chứng minh Tứ giác MDIB nội tiếp.
Cho ΔABC ( góc A= 900) có AB= 5cm , AC= 12cm . Xác định tâm , bán kính đường tròn ngoại tiếp ΔABC
giải chi tiết giúp mk vớiiiii ạ
Khẳng định nào sau đây đúng?
a)Qua ba điểm không thẳng hàng vẽ được vô số đường tròn
b) Qua hai điểm phân biệt vẽ được vô số đường tròn.
c)Một đường được xác định nếu biết tâm của nó.
d)Một đường tròn được xác định nếu biết bán kính của nó
