Để hàm số có TXĐ là R thì \(mx^2-2mx+5m+2>=0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\m>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-2m\right)^2-4m\left(5m+2\right)< =0\\m>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m^2-20m^2-8m< =0\\m>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-16m^2-8m< =0\\m>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-8m\left(2m+1\right)< =0\\m>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>0\\m\left(2m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m+1>=0\end{matrix}\right.\)
=>m>0
=>Giá trị nguyên nhỏ nhất của m thỏa mãn là m=1


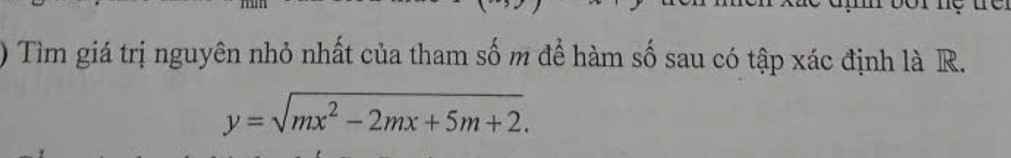




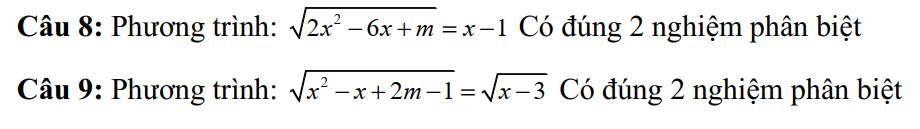 HELPPP
HELPPP




