Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{2x+y-3z}{2\cdot2+3-3\cdot5}=\dfrac{-8}{-8}=1\\ \Rightarrow x=2\cdot1=2\\ y=3\cdot1=3\\ z=5\cdot1=5\)
Vậy ...
Ta có: `x/2 = y/3 = z/5 = (2x)/4 = (3z)/15`
Áp dụng tính chất dãy tỉ số bằng nhau
`=> x/2 = y/3 = z/5 = (2x)/4 = (3z)/15 = (2x + y - 3z)/(4 + 3 - 15) = (-8)/(-8) = 1`
Khi đó: `{(x/2=1),(y/3=1),(z/5=1):}`
`=> {(x=2),(y=3),(z=5):}`
Vậy ...


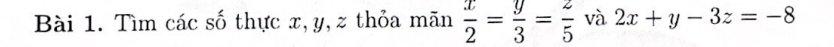 HELP
HELP
















