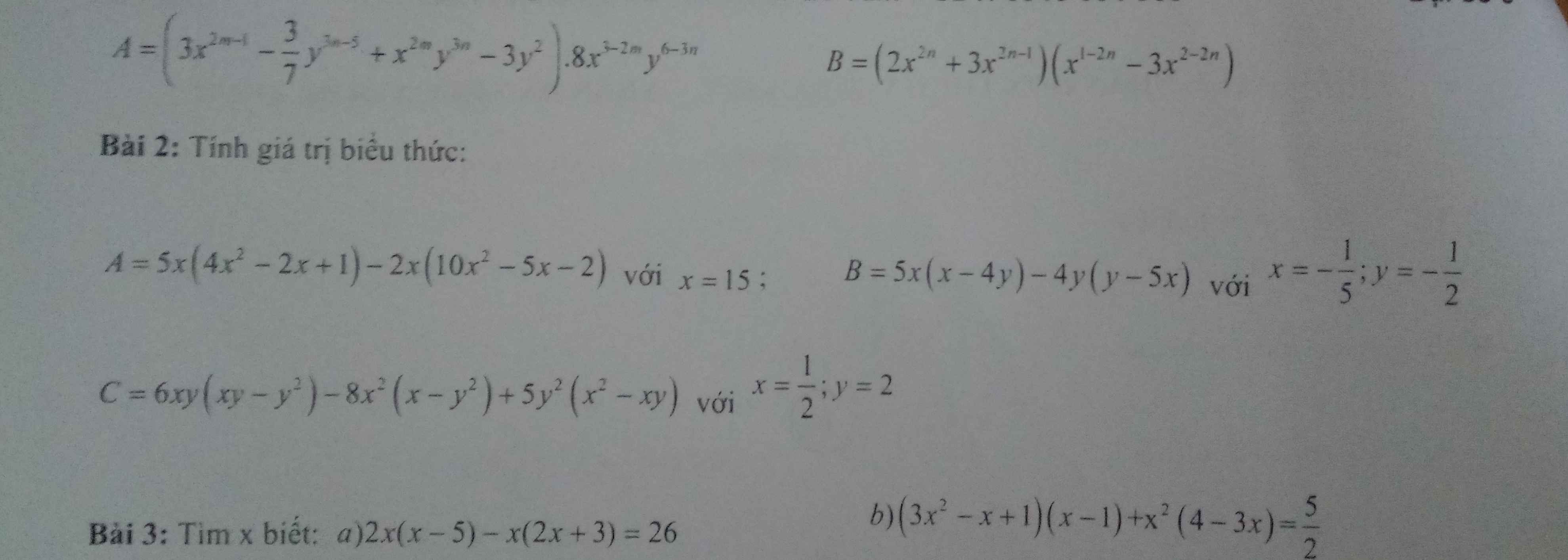Áp dụng TCDSTLBN, ta có :
\(\dfrac{a}{b+c}=\dfrac{b}{c+a}=\dfrac{c}{a+b}=\dfrac{a+b+c}{b+c+c+a+a+b}=\dfrac{1}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{b+c}=\dfrac{1}{2}\\\dfrac{b}{c+a}=\dfrac{1}{2}\\\dfrac{c}{a+b}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{b+c}{a}=2\\\dfrac{c+a}{b}=2\\\dfrac{a+b}{c}=2\end{matrix}\right.\)
\(Q=\left(1+\dfrac{a}{b}\right)\left(1+\dfrac{b}{c}\right)\left(1+\dfrac{c}{a}\right)\)
\(Q=\dfrac{a+b}{b}.\dfrac{b+c}{c}.\dfrac{c+a}{a}=2.2.2=8\)
Vậy \(Q=8\)
Bài này cũng như bài trước, cần xét cả trường hợp \(a+b+c=0\)
Khi đó \(\left\{{}\begin{matrix}b+c=-a\\c+a=-b\\a+b=-c\end{matrix}\right.\)
\(Q=\dfrac{\left(a+b\right)}{b}.\dfrac{\left(b+c\right)}{c}.\dfrac{c+a}{a}=\dfrac{\left(-c\right).\left(-a\right).\left(-b\right)}{abc}=-1\)


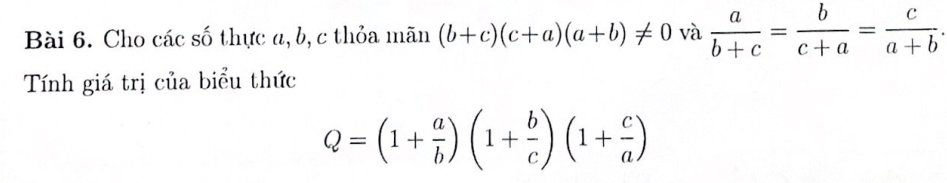 Help me
Help me