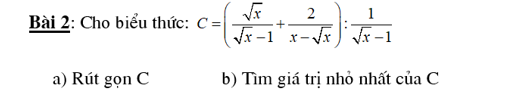\(x+y-2\sqrt{x-1}-4\sqrt{y-2}+2=0\left(1\right)\) đk: \(x\ge1;y\ge2\)
Đặt: \(a=\sqrt{x-1};b=\sqrt{y-2}\left(2\right)\)
\(\Rightarrow a^2+b^2=x+y-3\Leftrightarrow x+y=a^2+b^2+3\left(3\right)\)
thay (2)(3) vào (1) ta có:
\(a^2+b^2-2a-4b+5=0\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-4b+4\right)=0\Leftrightarrow\left(a-1\right)^2+\left(b-2\right)^2=0\Leftrightarrow\left\{{}\begin{matrix}a-1=0\\b-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{y-2}=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=2\\y=6\end{matrix}\right.\left(tm\right)}}\)
\(a^2+b^2+3-2a-4a+2=0\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-4b+4\right)=0\Leftrightarrow\left(a-1\right)^2+\left(b-2\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-1=0\\b-2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{y-2}=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=6\end{matrix}\right.\)\(\left(tm\right)\)



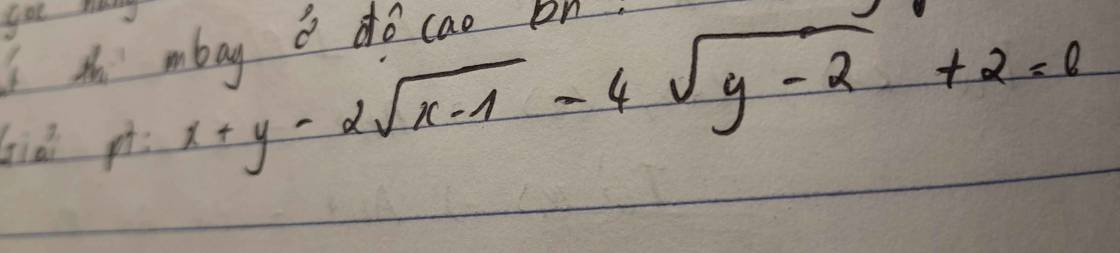



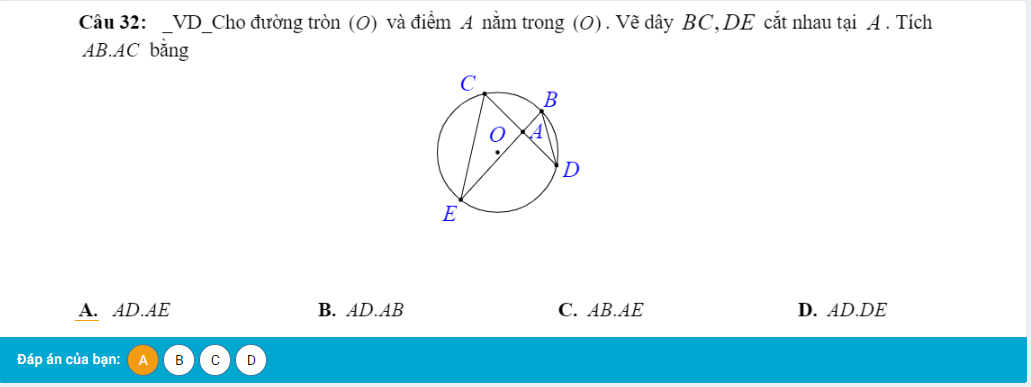



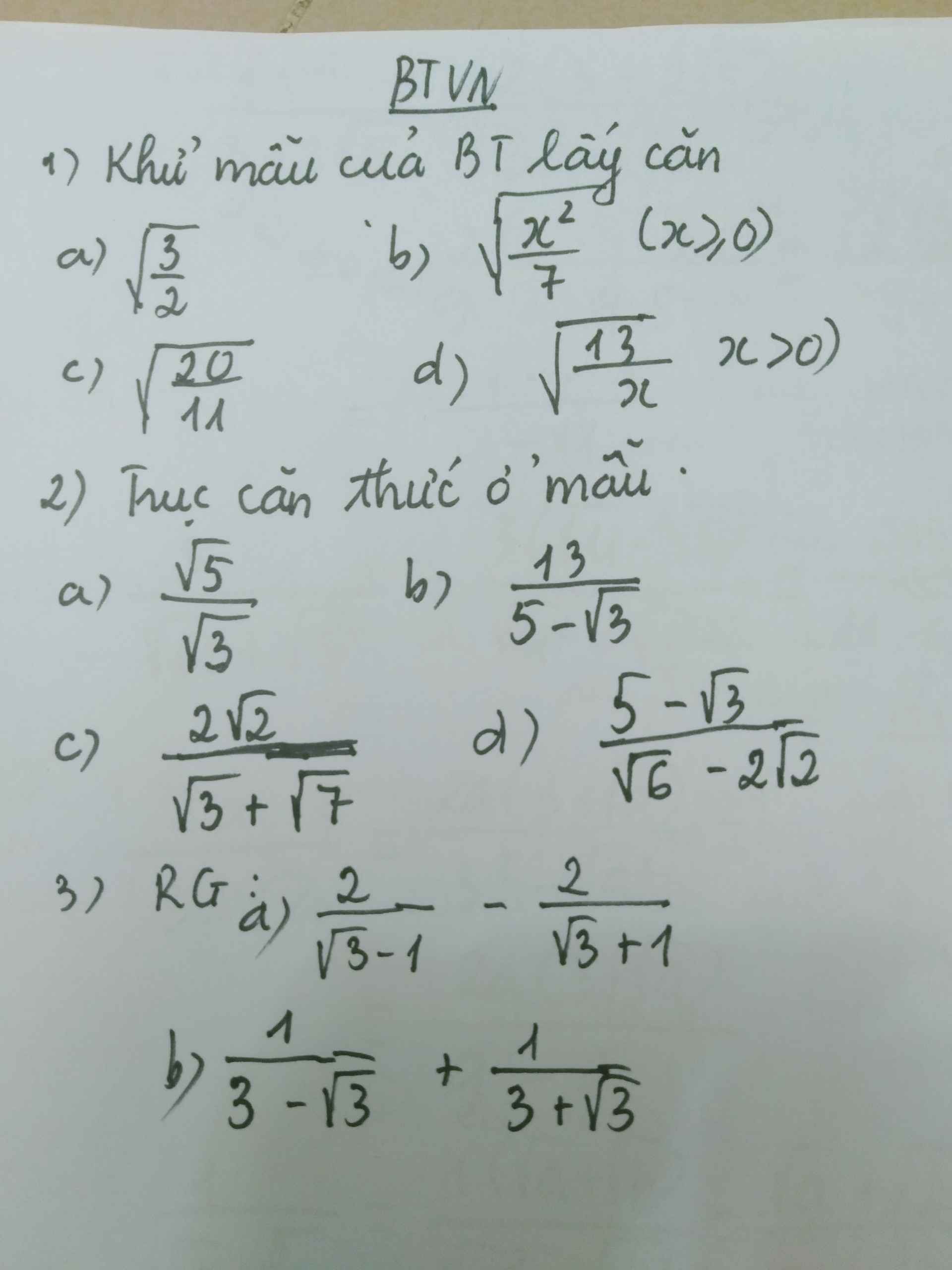

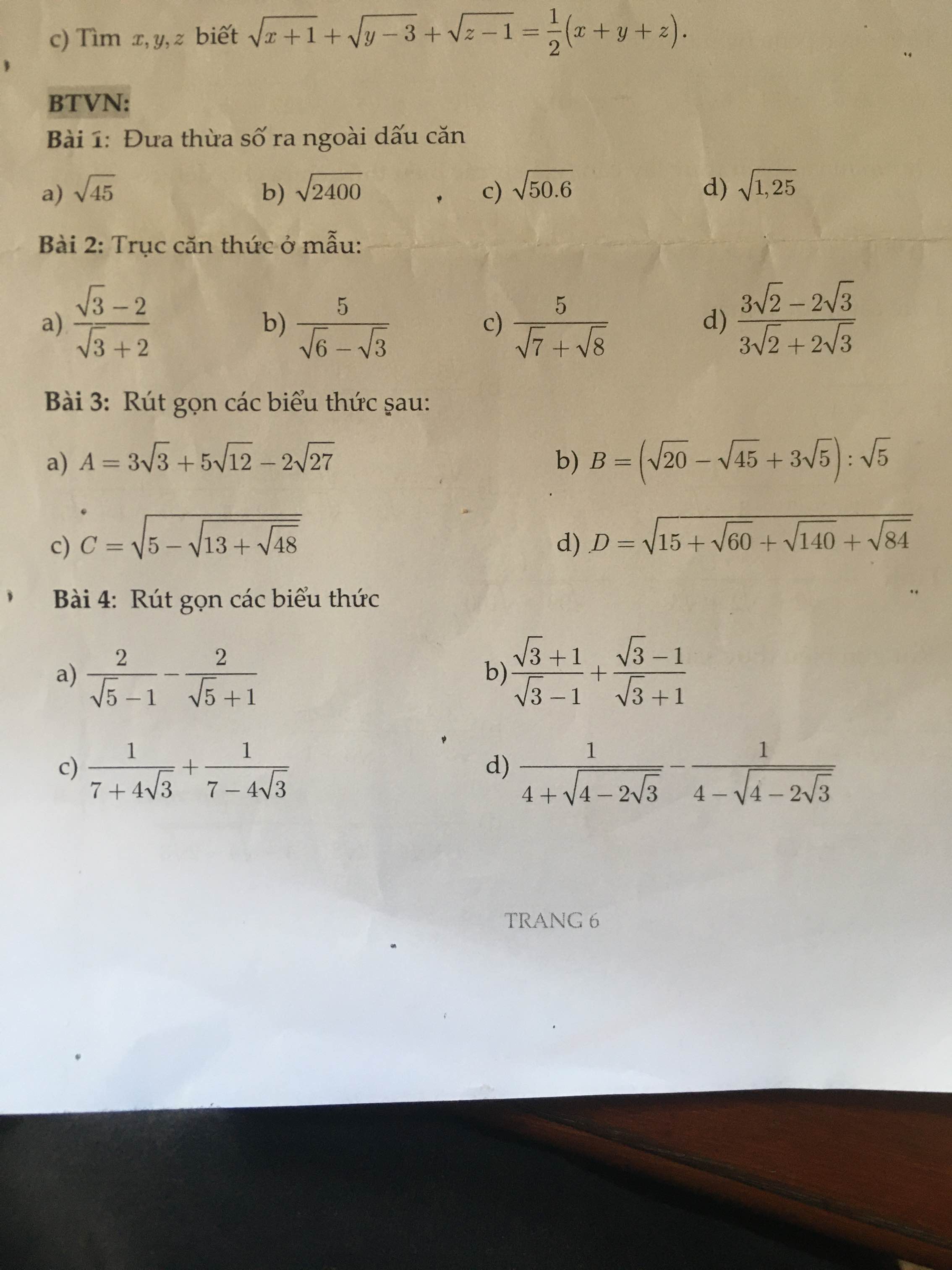

 HELP ME
HELP ME