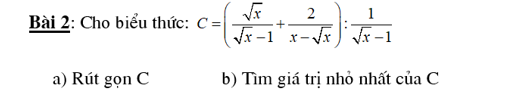a: Vì AB,EF là các đường kính của (O)
nên AB=EF
Xét tứ giác AEBF có
O là trung điểm chung của AB và EF
=>AEBF là hình bình hành
Hình bình hành AEBF có AB=EF
nên AEBF là hình chữ nhật
b: AEBF là hình chữ nhật
=>\(\hat{AEB}=\hat{AFB}=90^0\)
=>BE⊥AN tại E và BF⊥AK tại F
Xét ΔABK vuông tại B có BF là đường cao
nên \(AF\cdot AK=AB^2\left(1\right)\)
Xét ΔABN vuông tại B có BE là đường cao
nên \(AE\cdot AN=AB^2\left(2\right)\)
Từ (1),(2) suy ra \(AF\cdot AK=AE\cdot AN\)
=>\(\frac{AF}{AN}=\frac{AE}{AK}\)
Xét ΔAFE vuông tại A và ΔANK vuông tại A có
\(\frac{AF}{AN}=\frac{AE}{AK}\)
Do đó: ΔAFE~ΔANK
=>\(\hat{AFE}=\hat{ANK}\)
mà \(\hat{AFE}+\hat{EFK}=180^0\) (hai góc kề bù)
nên \(\hat{EFK}+\hat{ENK}=180^0\)
=>EFKN là tứ giác nội tiếp






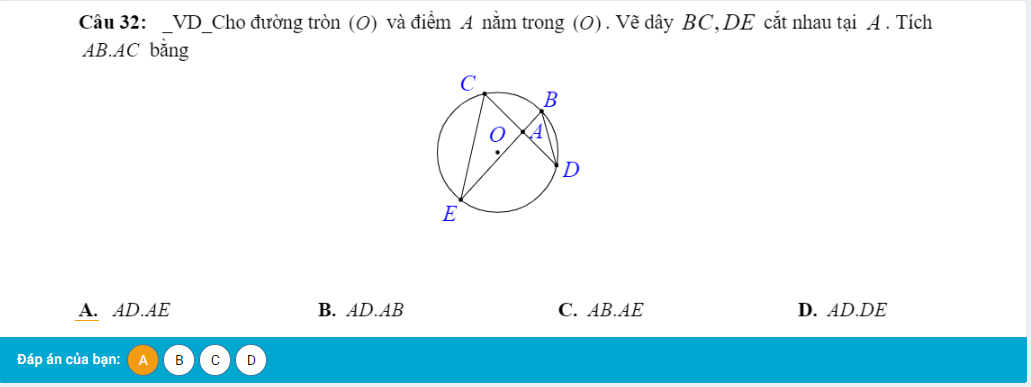

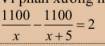


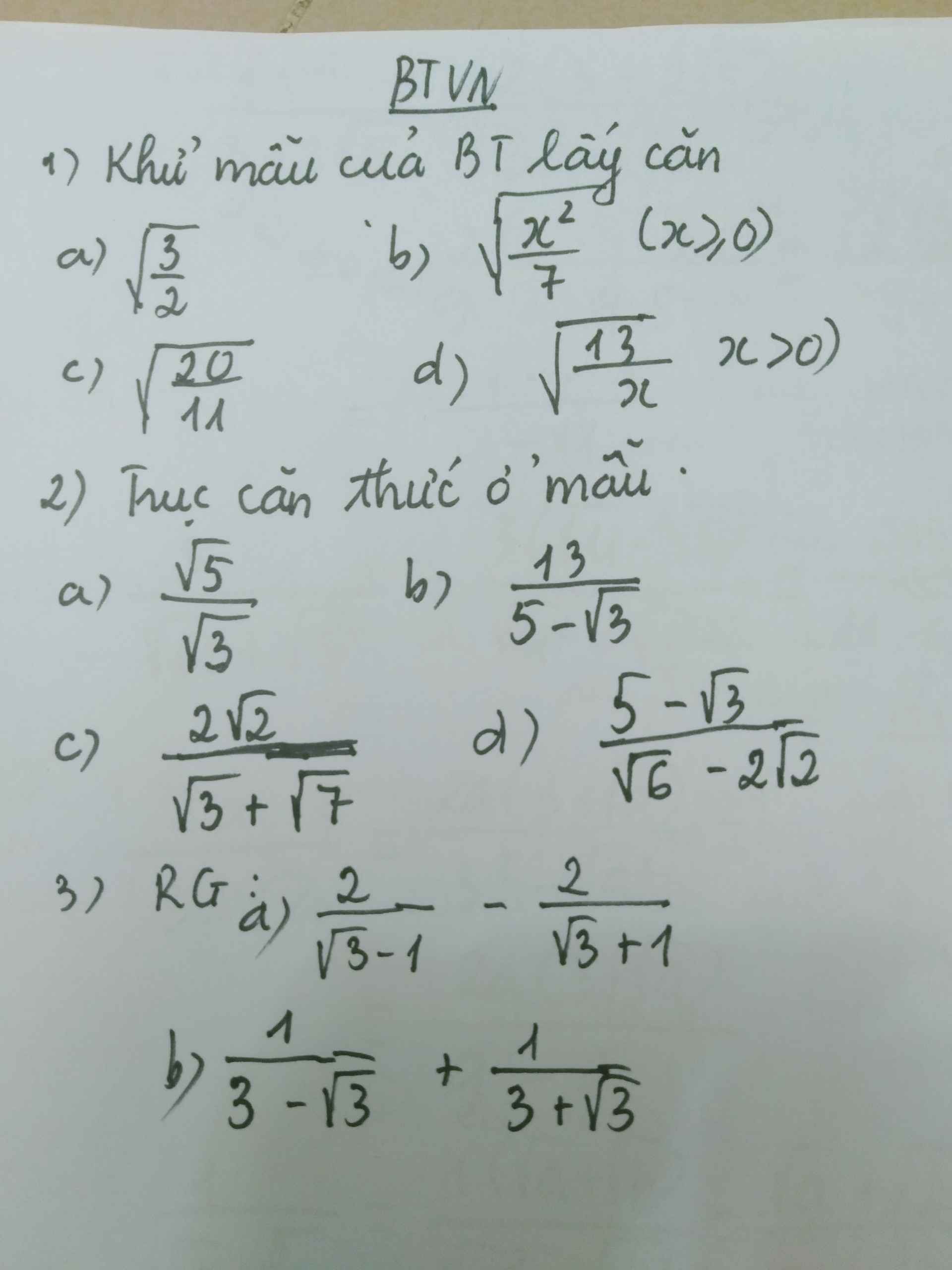


 HELP ME
HELP ME