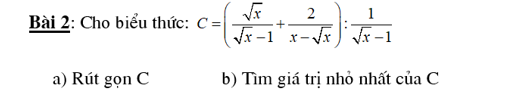Bài 11 :
Gọi \(x,y,z\left(m\right)\) lần lượt là cạnh \(AB,AC,BC\) của tam giác ABC
\(\left(0< x,y,z< 12\right)\)
Theo đề bài, ta có hệ pt :
\(\left\{{}\begin{matrix}x+y+z=12\left(1\right)\\x^2+y^2+z^2=50\left(2\right)\end{matrix}\right.\)
Theo d/l Pytago : \(x^2+y^2=z^2\) \(\left(3\right)\)
\(\left(2\right),\left(3\right)\Rightarrow z^2+z^2=50\Rightarrow2z^2=50\Rightarrow z=5\left(tmdk\right)\)
Thay \(z=5\) vào hệ pt \(\left(1\right),\left(2\right)\) ta có :
\(\left\{{}\begin{matrix}x+y+5=12\\x^2+y^2+5^2=50\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=7\\x^2+y^2=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=7-y\\\left(7-y\right)^2+y^2=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=7-y\\49-14y+y^2+y^2=25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=7-y\\2y^2-14y+24=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=7-y\\y^2-7y+12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=7-y\left(4\right)\\\left\{{}\begin{matrix}y=4\left(tmdk\right)\\y=3\left(tmdk\right)\end{matrix}\right.\end{matrix}\right.\)
Thay \(y=4\) vào \(\left(4\right)\) ta có \(x=7-4=3\left(tmdk\right)\)
Thay \(y=3\) vào \(\left(4\right)\) ta có \(x=7-3\left(tmdk\right)\)
Vậy độ dài cạnh AB,AC,BC lần lượt là \(3cm,4cm,5cm\) hoặc \(4cm,3cm,5cm\)
Bài 12 :
Gọi \(x\left(m\right)\) là chiều dài của hình chữ nhật \(\left(0< x< 600\right)\)
\(\dfrac{600}{x}\left(m\right)\) là chiều rộng của hình chữ nhật
Theo đê bài, ta có pt :
\(\left(x-4\right)\left(\dfrac{600}{x}-4\right)=416\)
\(\Leftrightarrow\left(x-4\right)\left(\dfrac{600-4x}{x}\right)=416\)
\(\Leftrightarrow\dfrac{600x-4x^2-2400+16x-416x}{x}=0\)
\(\Leftrightarrow-4x^2+200x-2400=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\x=20\end{matrix}\right.\)(tmdk)
Vậy vườn trường hình chữ nhật có kích thước của chiều dài là \(30m\), chiều rộng là \(\dfrac{600}{30}=20m\)
hoặc chiều dài là \(20m\), chiều rộng là \(\dfrac{600}{20}=30m\)







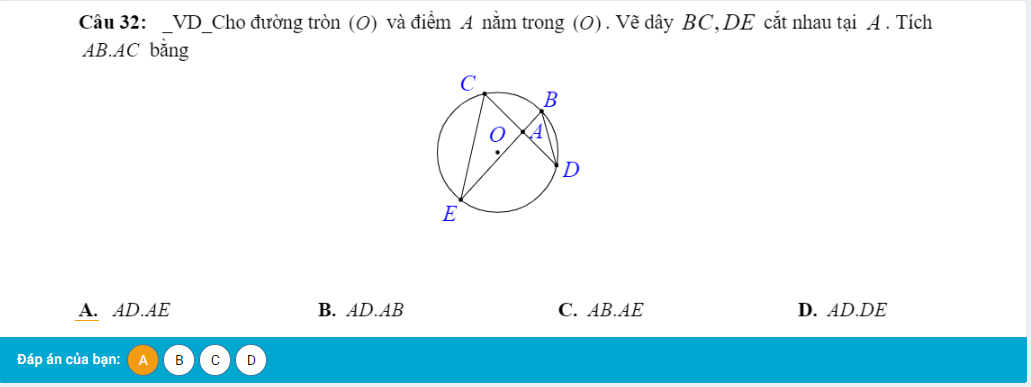

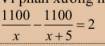


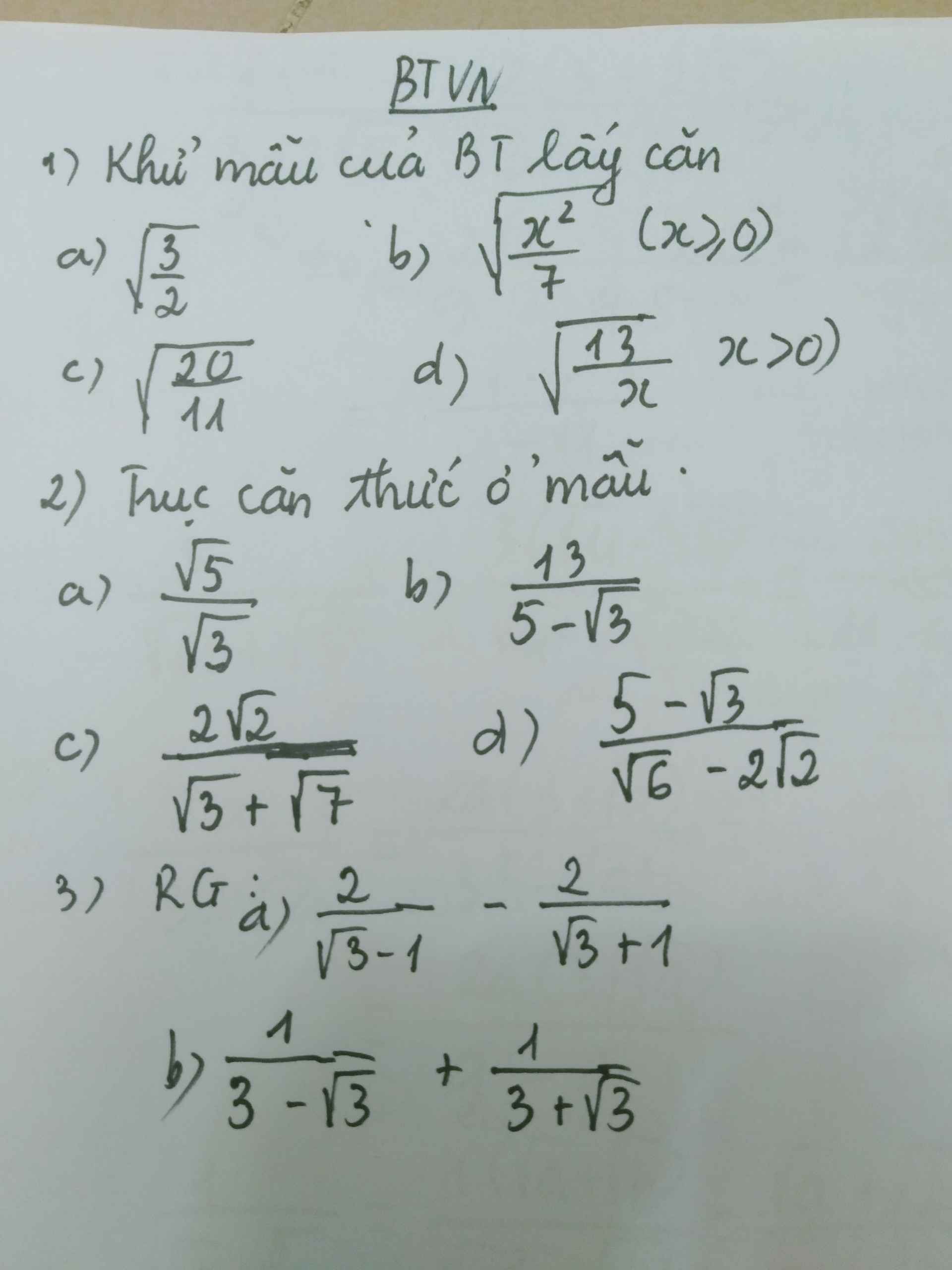


 HELP ME
HELP ME