Chọn đáp án B
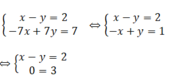
⇒ Hệ phương trình đã cho vô nghiệm ⇒ S = ∅
Cách 2: Ta thấy: 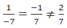 ⇒ Hệ pt vô nghiệm
⇒ Hệ pt vô nghiệm
Chọn đáp án B
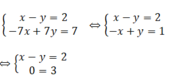
⇒ Hệ phương trình đã cho vô nghiệm ⇒ S = ∅
Cách 2: Ta thấy: 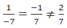 ⇒ Hệ pt vô nghiệm
⇒ Hệ pt vô nghiệm
cho hệ phương trình \(\hept{\begin{cases}\text{x+my=2}\\\text{mx-y=1}\end{cases}}\)
a) tìm số nguyên m để hệ có nghiệm (x;y) thỏa mãn x>0 và y<0
b) tìm giá trị lớn nhất của biểu thức S = 2x-y với (x;y) là nghiệm của hệ phương trình đã cho.
Cho hệ phương trình: mx + 4y = 10 - m và x + my = 4 (m là tham số)
tìm m để hệ có nghiệm duy nhất (x;y) sao cho S = x^2 - y^2 đat Min
giải các hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{2x+1}{4}-\dfrac{y-2}{3}=\dfrac{1}{12}\\\dfrac{x+5}{2}=\dfrac{y+7}{3}-4\end{matrix}\right.\)
b2.
\(A=\sqrt{3+\sqrt{5}}+\sqrt{7-3\sqrt{5}}-\sqrt{2}\)
B3. Tìm ĐKXĐ
\(\dfrac{1}{x\sqrt{x}+1}-\dfrac{2}{\sqrt{x}+1}\)
b4. so sánh A với 1
A=\(\dfrac{\sqrt{x}}{x-\sqrt{x}+1}\)
b5.tính
a,\(\sin47+2\sin38-\cos43-\cos52\)
b, \(C=\dfrac{2\sin^2x-1}{\sin x-\cos x}\)
phưcho phương trình x2 - 2 ( 2m + 1 )x + 3 + 4m = 0 (1)
a > Tìm hệ thức giữa x1 S x2 độc lập với m .
b > Tính m biểu thức A = X13 + X23.
c > Tìm m để (1) có 1 nghiệm gấp 3 lần nghiệm kia .
d > Lập phương trình bậc hai có các nghiệm là X12 , X22
cho hệ phương trình \(\left\{{}\begin{matrix}x+y=2\\\left(m+1\right)x+my=7\end{matrix}\right.\)
a) chứng minh rằng: với mọi m thì hệ phương trình luôn có nghiệm x,y thỏa mãn x.y =< 1
b) tìm m là số nguyên để hệ phương trình có nghiệm thỏa mãn x.y>0
cho hệ phương trình {a^2x-y=-7 và 2x+y=1
1,giải hệ phương trình khi a=1
2,gọi(x,y)là nghiệm. tìm a để x+y=2
cho hệ phương trình\(\hept{\begin{cases}3x-my=-9\\mx+2y=16\end{cases}}\)
a) giải hệ phương trình khi m = 5
b) chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m
c) định m để hệ có nghiệm (x ; y) = (1,4 ; 6,6)
d) với trị nguyên nào của m để hệ có nghiệm (x ; y) thỏa mãn x + y = 7
Giải phương trình nghiệm nguyên , x^2 - y^2 = p ^ s trong đó p là số nguyên tố , s là số nguyên dương .
cho hệ phương trình: \(\hept{\begin{cases}x+my=2m^2\\x-y=m^2+1\end{cases}}\)
tìm m để hệ phương trình có nghiệm duy nhất (x;y) sao cho biểu thức S= \(\sqrt{x}+\sqrt{y}\) đạt giá trị nhỏ nhất