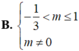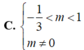\(y=x^2-mx+m-1\)
\(\Delta\ge0\Leftrightarrow m^2-4\left(m-1\right)\ge0\Leftrightarrow m^2-4m+4\ge0\left(luôn-đúng\right)\)
\(vi-ét\Rightarrow\left\{{}\begin{matrix}x1+x2=m\\x1x2=m-1\end{matrix}\right.\)
\(P=\dfrac{2x1x2+3}{x1^2+x2^2+2x1x2+2}=\dfrac{2m-2+3}{\left(x1+x2\right)^2+2}=\dfrac{2m+1}{m^2+2}\)
\(\Leftrightarrow P\left(m^2+2\right)=2m+1\)
\(\Leftrightarrow Pm^2-2m+2P-1=0\)
\(TH1:P=0\Rightarrow-2m-1=0\Leftrightarrow m=-\dfrac{1}{2}\Rightarrow maxP=0\)
\(TH2:P\ne0\Rightarrow\Delta\ge0\Leftrightarrow4-4P\left(2P-1\right)\ge0\)
\(\Leftrightarrow-8P^2+4P+4\ge0\Leftrightarrow-\dfrac{1}{2}\le P\le1\Rightarrow maxP=1\)
\(\Rightarrow maxP=1\Leftrightarrow m=1\)