Các câu hỏi tương tự
Cho hàm số y f(x) liên tục trên R và thỏa mãn f(-1)0f(x) Gọi S là diện tích hình phẳng giới hạn bởi các đường yf(x); y0; x-1 và x1Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(-1)>0<f(x) Gọi S là diện tích hình phẳng giới hạn bởi các đường y=f(x); y=0; x=-1 và x=1Mệnh đề nào sau đây đúng?
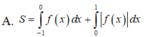
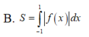
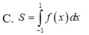
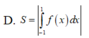
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau:
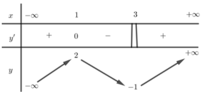
Số nghiệm của phương trình f(x) + 1 = 0 là:
A. 3.
B. 0.
C. 1.
D. 2.
Tìm các khoảng đồng biến của hàm số: y = 2sinx + cos2x, x ∈ [0;π] A. (0; pi/2 B. (pi/2; pi) C. (0; pi/6) và pi/2; 5pi/6) D. (0;pi).
Hàm số \(y=-x^3+3x^2-4\) đồng biến trên tập hợp nào sau đây:
A:(2;+∞)
B:(0;2)
C:(-∞;0)\(\cup\) (2;+∞)
D:(-∞;0)
Trong không gian \(Oxyz\) ,cho đường thẳng \(d:\dfrac{x}{-1}=\dfrac{y-1}{2}=\dfrac{z-1}{-5}\) và mặt phẳng \(\left(P\right):x-2y+5z-1=0\).Số mặt phẳng chứa \(d\) và vuông góc với mặt phẳng \(\left(P\right)\) là
Cho hàm số yf(x) có bảng biến thiên như hình vẽ.Khi đó phương trình f(x) +1m có ba nghiệm thực phân biệt khi và chỉ khi A. 1m2 B.
1
≤
m
≤
2
C.
0
≤
m
≤
1
D. 0m1
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
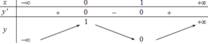
Khi đó phương trình f(x) +1=m có ba nghiệm thực phân biệt khi và chỉ khi
A. 1<m<2
B. 1 ≤ m ≤ 2
C. 0 ≤ m ≤ 1
D. 0<m<1
Cho hàm số f(x) có đạo hàm f'(x) = \(x\left(1-x\right)^2\left(3-x\right)^3\left(x-2\right)^4\) . Điểm cực tiểu của hàm số đã cho là
A: x = 2
B: x = 3
C: x = 0
D: x = 1
Ai có bảng biến thiên thì vẽ cho dễ hiểu
Cho hàm số y f(x) thỏa mãn f(-2) -2, f(2) 2 và có bảng biến thiên như hình bên Có bao nhiêu số tự nhiên m thỏa mãn bất phương trình
f
-
f
x
≥
≥
m
có nghiệm thuộc đoạn [-1;1]? A. 1. B. 2. C. 3. D. 4.
Đọc tiếp
Cho hàm số y = f(x) thỏa mãn f(-2) = -2, f(2) = 2 và có bảng biến thiên như hình bên
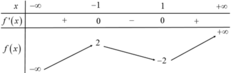
Có bao nhiêu số tự nhiên m thỏa mãn bất phương trình f - f x ≥ ≥ m có nghiệm thuộc đoạn [-1;1]?
A. 1.
B. 2.
C. 3.
D. 4.
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) (x-6)
x
2
+
4
trên đoạn [0;3] có dạng a - b
c
với a là số nguyên và b, c là các số nguyên dương. Tính S a + b + c. A. 4 B. -2 C. -22 D. 5
Đọc tiếp
Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) = (x-6) x 2 + 4 trên đoạn [0;3] có dạng a - b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c.
A. 4
B. -2
C. -22
D. 5








