Chọn C.
Do f ' x > 0 , ∀ x ∈ 4 ; 7
⇒ f x đồng biến trên khoảng 4 ; 7 .
⇒ f 6 > f 5
Chọn C.
Do f ' x > 0 , ∀ x ∈ 4 ; 7
⇒ f x đồng biến trên khoảng 4 ; 7 .
⇒ f 6 > f 5
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số f(x) có đạo hàm trên ℝ và f''(x) > 0, ∀ x ∈ ℝ . Biết f(1) = 2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2) + f(3) = 4
B. f(-1)= 2
C. f(2) = 1
D. f(2018) > f(2019)
Cho hàm số f(x) có đạo hàm trên ℝ thỏa mãn f’(x) – 2018f(x) = 2018.x2017.e2018x với mọi x ∈ ℝ và f(0) = 2018. Tính giá trị f(1).
A. f(1) = 2019e2018.
B. f(1) = 2018e-2018.
C. f(1) = 2018e2018.
D. f(1) = 2017e2018.
Cho hàm số f(x) có đạo hàm trên R thỏa mãn f'(x)-2018f(x)= 2018 x 2017 e 2018 x với mọi x ∈ ℝ , f(0)=2018. Tính f(1)
![]()
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn f(x) > 0, ∀ x ∈ ℝ . Biết f(0) = 1 và f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
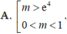
![]()
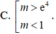
![]()
Cho hàm số y=f(x) có đạo hàm trên ℝ thỏa mãn 3 f ' ( x ) . e f 3 ( x ) - x 2 - 1 - 2 x f 2 ( x ) = 0 và f(0)=1 . Tích phân ∫ 0 7 x . f ( x ) d x bằng:
A. 2 7 3
B. 15 4
C. 45 8
D. 5 7 4
Cho a , b ∈ ℝ , 0 < a < b, hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f'(x) < 0, ∀ x ∈ ( a ; b ) . Giá trị nhỏ nhất của hàm số đã cho trên đoạn [a;b] bằng
A. f(b)
B. f a + b 2
C. f(a)
D. f a b
Cho hàm f có tập xác định là K ⊂ ℝ , đồng thời f có đạo hàm f’(x) trên K. Xét hai phát biểu sau:
(1) Nếu f ' x 0 ≠ 0 thì x 0 không là điểm cực trị của hàm f trên K.
(2) Nếu x 0 mà f’(x) có sự đổi dấu thì x 0 là điểm cực trị của hàm f.
Chọn khẳng định đúng
A. (1), (2) đều đúng.
B. (1), (2) đều sai.
C. (1) sai, (2) đúng.
D. (1) đúng, (2) sai.
Cho hàm số y=f(x) có đạo hàm trên ℝ . Bảng biến thiên của hàm số y=f'(x) như hình dưới
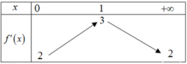
Tìm m để bất phương trình m + 2 sin x ≤ f ( x ) nghiệm đúng với mọi x ∈ 0 ; + ∞ .
A. m < f(0) +1
B. m < f(1)
C. m < f(0)
D. m < f(0) -1