Chọn C.
- Ta có:
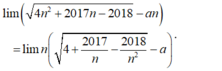
- Vì:
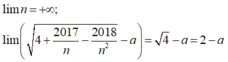
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
Chọn C.
- Ta có:
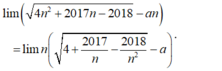
- Vì:
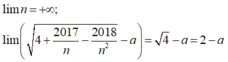
- Suy ra:  có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
có giá trị hữu hạn nếu 2 - a = 0 hay a = 2.
Gọi S là tập các số nguyên của a sao cho l i m 4 n 2 + 2017 n - 2018 - a n có giá trị hữu hạn. Tính tổng các phần tử của S.
A. S = 4
B. S = 0
C. S = 2
D. S = 1
Cho hàm số y = 4 3 . sin 3 x + 2 . cos 2 x - ( 2 m 2 - 5 m + 2 ) . sin x - 2017 . Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số đồng biến trên khoảng 0 , π 2 . Tìm số phần tử của S.
A. 0
B. 1
C. 2
D. Vô số.
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình cos 2 x − π 3 − m = 2 có nghiệm. Tính tổng T của các phần tử trong S.
A T= 6
B. T = - 6
C. T = 2
D. T = - 4
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị hàm số y = x 3 - 3 x 2 tại 3 điểm phân biệt A, B, C (B nằm giữa A và C) sao cho AB=2BC. Tính tổng các phần tử thuộc
A. -2
B. -4
C. 0
D. 7 - 7 7
cho hàm số \(\dfrac{-x+2}{x-1}\) có đồ thị (C) và điểm A(a;1) . Gọi S là tập hợp tất cả các giá trị thực củ tham số a để có đúng 1 tiếp tuyến của (C) đi qua A. Tổng tất cả các giá trị của S là
Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số y = 4x + (m+1)sinx+ mcosx đồng biến trên ℝ Số phần tử của S là.
A. 4.
B. 6.
C. 5.
D. Vô số.
Cho phương trình  Gọi S là tập hợp tất cả các giá trị thực của
α
thuộc đoạn
0
;
2
π
để phương trình có nghiệm. Tổng các phần tử của tập S bằng
Gọi S là tập hợp tất cả các giá trị thực của
α
thuộc đoạn
0
;
2
π
để phương trình có nghiệm. Tổng các phần tử của tập S bằng
A. π
B. 2
C. 4 π
D. 6 π
Cho tập A = 1 , 2 , . . . , 100 . Gọi S là tập hợp tất cả các tập con của A, mỗi tập con gồm 2 phần tử có tổng bằng 100. Chọn ngẫu nhiên một phần tử thuộc S. Xác suất để chọn được phần tử có tích hai số là một số chính phương bằng
A. 6 49
B. 4 99
C. 4 49
D. 2 33
gọi s là tập hợp các giá trị của m để hàm số \(y=x^2+\left(m+1\right)x+2021m+2022\) đồng biến trên khoảng (-2,+\(\infty\) )
khi đó tập họp (-2020;2021)\(\cap S\) có bao nhiêu phần tử