Các câu hỏi tương tự
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SC. Gọi I là giao điểm của đường thẳng AM với mặt phẳng (SBD). Khi đó tỉ số \(\dfrac{MA}{IA}\) bằng bao nhiêu?
Xem chi tiết
A. \(\dfrac{4}{3}\)
B. 3
C. 2
D. \(\dfrac{3}{2}\)
Trong không gian xét
m
→
;
n
→
;
p
→
;
q
→
là những vectơ đơn vị (có độ dài bằng 1). Gọi M là giá trị lớn nhất của biểu thức
m
→
-
n...
Đọc tiếp
Trong không gian xét m → ; n → ; p → ; q → là những vectơ đơn vị (có độ dài bằng 1). Gọi M là giá trị lớn nhất của biểu thức m → - n → 2 + m → - p → 2 + m → - q → 2 + n → - p → 2 + n → - q → 2 + p → - q → 2 Khi đó M - M thuộc khoảng nào sau đây ?
A. 4 ; 13 2
B. 7 ; 19 2
C. 17 ; 22
D. 10 ; 15
Bài 2. (1 điểm) Trong hình sau, khi được kéo ra khơi vị trí cân bằng ờ điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$.
Tọa độ $s$ cm của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s10 sin left(10 t+dfrac{pi}{2}right)$. Vào các thời điểm nào thì $s-5 sqrt{3} $ cm?
Đọc tiếp
Bài 2. (1 điểm) Trong hình sau, khi được kéo ra khơi vị trí cân bằng ờ điểm $O$ và buông tay, lực đàn hồi của lò xo khiến vật $A$ gắn ở đầu của lò xo dao động quanh $O$.
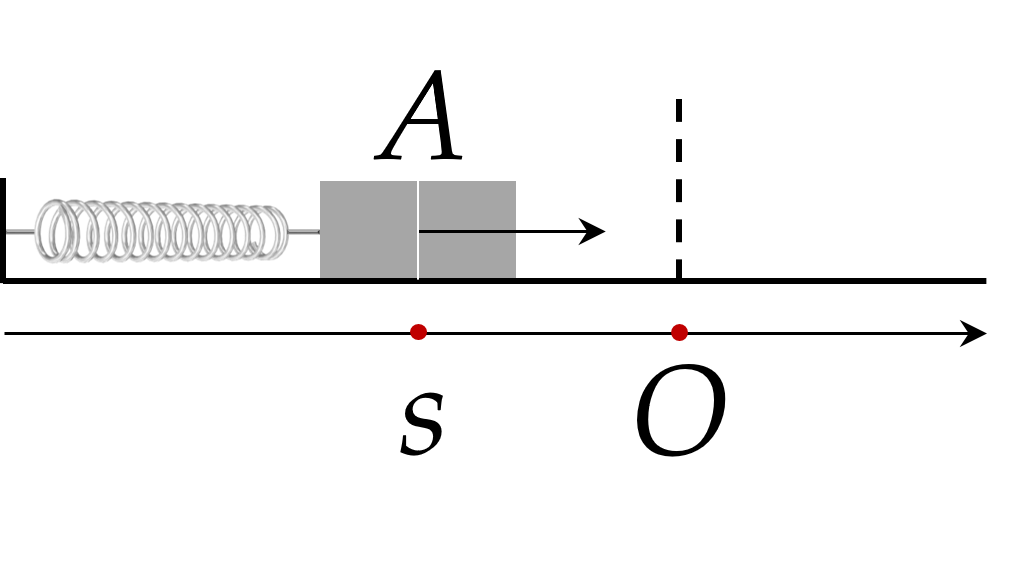
Tọa độ $s$ cm của $A$ trên trục $Ox$ vào thời điểm $t$ (giây) sau khi buông tay được xác định bởi công thức $s=10 \sin \left(10 t+\dfrac{\pi}{2}\right)$. Vào các thời điểm nào thì $s=-5 \sqrt{3} $ cm?
Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2, 3, 3, 2 (đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng?
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến M thành B, N thành C. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến B thành M, C thành N. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:
A. AD
B. BC
C. AC
D. MN
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (AMN) và mp (BCD) là:
A. ND
B. BC
C. CD
D. MN
Cho số nguyên dương n khi đó 2^2 + 4^2+... + (2n)^2 bằng








