Đáp án C
Áp dụng CT tính nhanh ta có S = − b 2 a . b 2 a = 1
Đáp án C
Áp dụng CT tính nhanh ta có S = − b 2 a . b 2 a = 1
Tìm giá trị của tham số m để đồ thị hàm số y=x4-2(m+1)x2+2m+3 có 3 điểm cực trị A,B,C là ba đỉnh của một tam giác, trục hoành chia tam gíac ABC thành một tam giác và một hình thang sao cho tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4/9
![]()
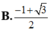
![]()
![]()
Cho hàm số y = x 4 - 2 x 2 + 4 . Gọi A,B,C là ba điểm cực trị của đồ thị hàm số. Tính diện tích S của tam giác ABC
A. 4.
B. 2.
C. 10.
D. 1.
Gọi A, B, C là ba điểm cực trị của đồ thị hàm số y = 2 x 4 - 4 x 2 + 1 . Diện tích tam giác ABC là
A. 3 2
B. 1
C. 3
D. 2
Cho đồ thị hàm số y = 1 3 x 4 - 2 x 2 - 1 có ba điểm cực trị là A, B, C. Biết M, N là hai điểm di động lần lượt thuộc các cạnh AB, AC sao cho diện tích tam giác ABC gấp ba lần diện tích tam giác AMN. Giá trị nhỏ nhất của độ dài đoạn thẳng MN là
A.. 2 3
B. 2 3 3
C. 4
D. 2
Tìm giá trị thực của tham số m để đồ thị hàm số y = x 4 - 2 ( m + 1 ) x 2 + 2 m + 3 ba điểm cực trị A,B,C sao cho trục hoành chia tam giác ABC thành hai đa giác sao cho: tỉ số giữa diện tích của tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4 9 .
A. m = - 1 + 15 2
B. m = - 1 + 3 2
C. m = 5 + 3 2
D. m = 1 + 15 2
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Gọi m1, m2 là các giá trị của tham số m để đồ thị hàm số y = 2x3 – 3x2 + m = 1 có hai điểm cực trị B, C sao cho tam giác OBC có diện tích bằng 2, với O là gốc tọa độ. Tính m1, m2
A. –20
B. –15
C. 12
D. 6
Gọi A,B,C là các điểm cực trị của đồ thị hàm số y = x 4 − 2 x 2 + 4. Bán kính đường tròn nội tiếp tam giác ABC bằng
A. 2 .
B. 1
C. 2 − 1.
D. 2 + 1.
Cho hàm số y = x 4 - 2 m 2 x 2 + 1 (1). Các giá trị m để đồ thị hàm số (1) có 3 điểm cực trị A, B, C và diện tích tam giác ABC bằng 1
A. ± 2
B. m = 1 , m = 3
C. m = ± 1
D. Đ á p á n k h á c