Do △ABC nhọn nên \(tanA,tanB,tanC>0\).
Ta chứng minh \(tanA+tanB+tanC=tanAtanBtanC\)
Thật vậy, ta có: \(tanA+tanB+tanC=tanA+tanB+tan\left(180^0-\widehat{A}-\widehat{B}\right)=tanA+tanB-tan\left(A+B\right)=tanA+tanB-\dfrac{tanA+tanB}{1-tanAtanB}=\left(tanA+tanB\right)\left(1-\dfrac{1}{1-tanAtanB}\right)=tanAtanB.\dfrac{tanA+tanB}{1-tanA.tanB}=tanAtanBtanC\left(đpcm\right)\)
a) Áp dụng bất đẳng thức Cauchy ta có:
\(tanA+tanB+tanC\ge3\sqrt[3]{tanAtanBtanC}=3\sqrt[3]{tanA+tanB+tanC}\)
\(\Rightarrow\sqrt[3]{\left(tanA+tanB+tanC\right)^2}\ge3\)
\(\Rightarrow tanA+tanB+tanC\ge\sqrt{3^3}=3\sqrt{3}\left(đpcm\right)\)
b) Ta có bất đẳng thức đúng với mọi x,y,z là các số thực: \(x^2+y^2+z^2\ge\dfrac{\left(x+y+z\right)^2}{3}\)
Áp dụng bất đẳng thức trên ta được:
\(tan^2A+tan^2B+tan^2C\ge\dfrac{\left(tanA+tanB+tanC\right)^2}{3}\ge\dfrac{\left(3\sqrt{3}\right)^2}{3}=9\left(đpcm\right)\)
Đẳng thức xảy ra khi \(tanA=tanB=tanC\) \(\Leftrightarrow\Delta ABC\) đều











 Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ









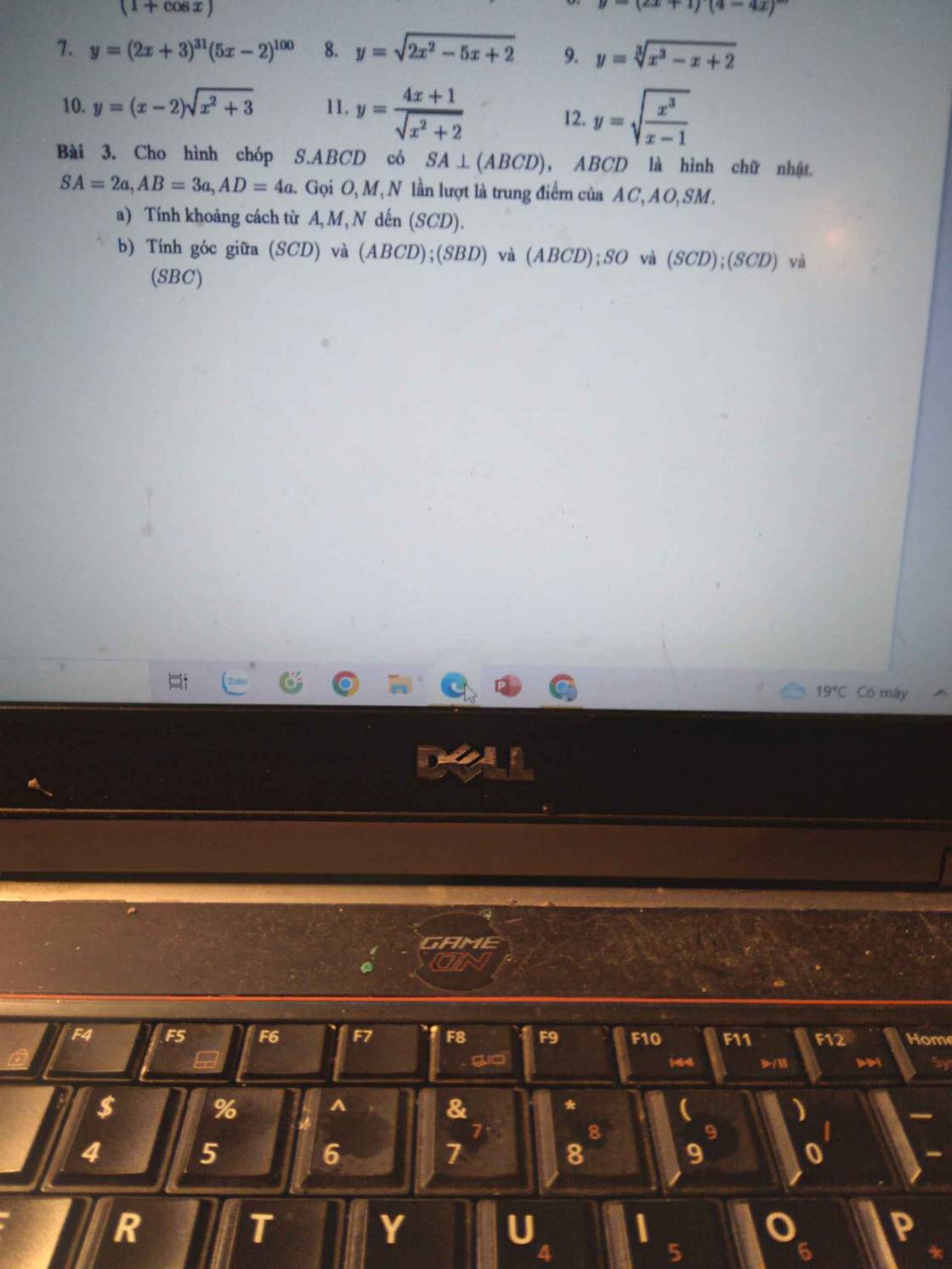 Giúp em bài 3 với ạ. Em cảm ơn ạ
Giúp em bài 3 với ạ. Em cảm ơn ạ