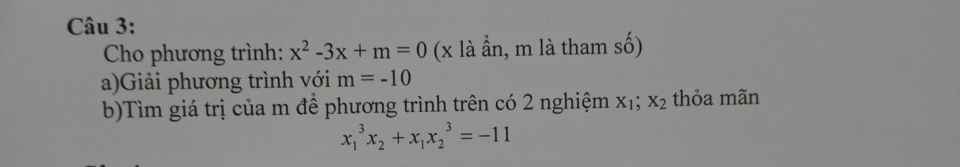\(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}=24+8\sqrt{5}-9+4\sqrt{5}=15+12\sqrt{5}\)
\(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}=17-12\sqrt{2}+9+4\sqrt{2}=26-8\sqrt{2}\)
\(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}=6-4\sqrt{2}+22-12\sqrt{2}=28-16\sqrt{2}\)
\(ô,\\ \Rightarrow24+8\sqrt{5}-\sqrt{\left(9-4\sqrt{5}\right)^2}\\ \Rightarrow24+8\sqrt{5}-\left(9-4-\sqrt{5}\right)\\ \Rightarrow24+8\sqrt{5}-9+4\sqrt{5}\\ \Rightarrow15+8\sqrt{5}+4\sqrt{5}\\ \Rightarrow15+12\sqrt{5}\)
\(ơ,\\ g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4+\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+9+4\sqrt{2}\)
\(u,\\ 6-4\sqrt{2}+\sqrt{\left(22-12\sqrt{2}\right)}^2\\ \Rightarrow6-4\sqrt{2}+22-12\sqrt{2}\\ \Rightarrow28-4\sqrt{2}-12\sqrt{2}\\ \Rightarrow28-16\sqrt{2}\)
ô \(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}\)
= 24 + 8\(\sqrt{5}\) - 9 + 4\(\sqrt{5}\)
= 15 + 12\(\sqrt{5}\)
ơ \(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}\)
= 17 - 12\(\sqrt{2}\) + 9 + 4\(\sqrt{2}\)
= 26 - 8\(\sqrt{2}\)
u \(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}\)
= 6 - 4\(\sqrt{2}\) + 22 - 12\(\sqrt{2}\)
= 28 -16\(\sqrt{2}\)

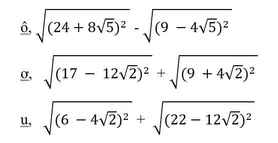








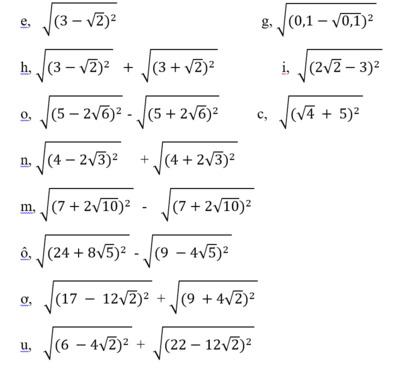
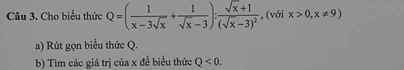
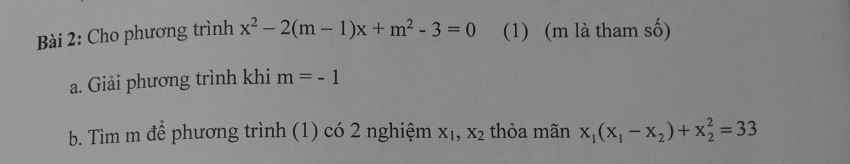


 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.