đây nha em
Bài 1:
a) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
hay AM\(\perp\)BC(đpcm)
b) Kẻ BK\(\perp\)AC và CH\(\perp\)AB
Ta có: M là trung điểm của BC(gt)
nên \(BM=CM=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow AM^2=10^2-6^2=64\)
hay AM=8(cm)
Xét ΔBHC vuông tại H và ΔBMA vuông tại M có
\(\widehat{HBC}\) chung
Do đó: ΔBHC\(\sim\)ΔBMA(g-g)
Suy ra: \(\dfrac{CH}{MA}=\dfrac{BC}{BA}\)(Các cặp cạnh tương ứng tỉ lệ)
\(\Leftrightarrow\dfrac{CH}{6}=\dfrac{12}{10}=\dfrac{6}{5}\)
hay CH=7,2(cm)
Xét ΔABK vuông tại K và ΔACH vuông tại H có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAK}\) chung
Do đó: ΔABK=ΔACH(Cạnh huyền-góc nhọn)
Suy ra: BK=CH(hai cạnh tương ứng)
mà CH=7,2cm(cmt)
nên BK=7,2cm
Bài 2:
a) Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔAMB và ΔANC có
AM=AN(cmt)
\(\widehat{BAM}\) chung
AB=AC(ΔABC cân tại A)
Do đó: ΔAMB=ΔANC(c-g-c)
Suy ra: BM=CN(hai cạnh tương ứng)
giúp em với ạ nhanh em cần ạ :33
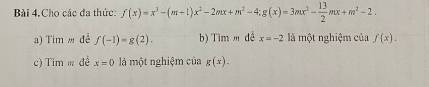
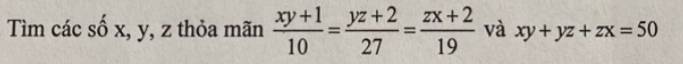
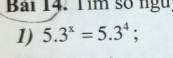gấp ạ nhanh cho em với:(((
