a: \(D=\left(-\dfrac{1}{7}\right)^0+\left(-\dfrac{1}{7}\right)^1+...+\left(-\dfrac{1}{7}\right)^{2017}\)
=>\(-\dfrac{1}{7}\cdot D=\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2018}\)
=>\(-\dfrac{1}{7}\cdot D-D=\left(-\dfrac{1}{7}\right)^1+\left(-\dfrac{1}{7}\right)^2+...+\left(-\dfrac{1}{7}\right)^{2018}-\left(-\dfrac{1}{7}\right)^0-\left(-\dfrac{1}{7}\right)^1-...-\left(-\dfrac{1}{7}\right)^{2017}\)
=>\(-\dfrac{8}{7}\cdot D=\left(-\dfrac{1}{7}\right)^{2018}-1=\dfrac{1}{7^{2018}}-1=\dfrac{1-7^{2018}}{7^{2018}}\)
=>\(D=\dfrac{7^{2018}-1}{7^{2018}}:\dfrac{8}{7}=\dfrac{7^{2018}-1}{7^{2017}\cdot8}\)
b: \(E=-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
=>\(3E=-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{49}}-\dfrac{1}{3^{50}}\)
=>\(3E+E=-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{49}}-\dfrac{1}{3^{50}}-\dfrac{1}{3}+\dfrac{1}{3^2}-...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)
=>\(4E=-1-\dfrac{1}{3^{51}}=\dfrac{-3^{51}-1}{3^{51}}\)
=>\(E=\dfrac{-3^{51}-1}{3^{51}\cdot4}\)
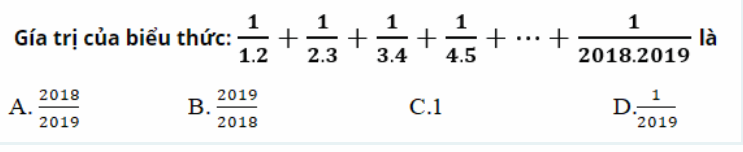
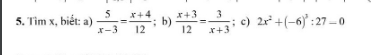
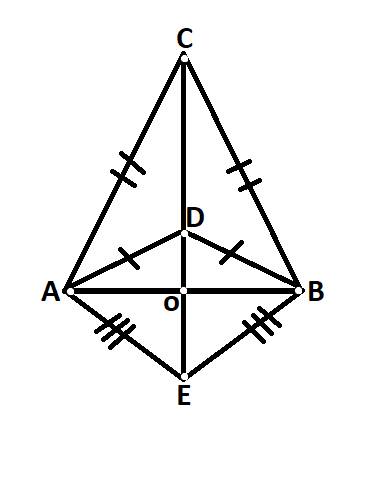
Giúp em bài này được không ạ! e cảm ơn nhìu ạ 
