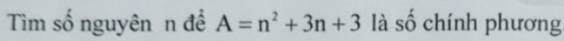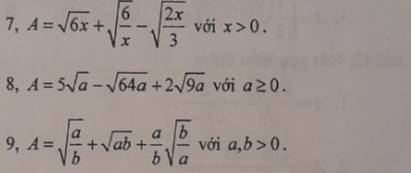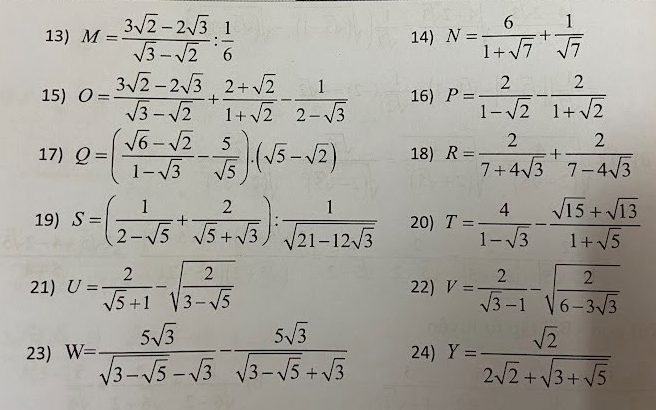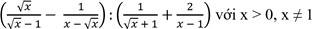A là số chính phương
=>\(n^2+3n+3=k^2\)
=>\(n^2+3n+\frac94+\frac34=k^2\)
=>\(\left(n+\frac32\right)^2-k^2=-\frac34\)
=>\(\left(2n+3\right)^2-4k^2=-3\)
=>(2n+3-2k)(2n+3+2k)=-3
=>(2n+3-2k;2n+3+2k)∈{(1;-3);(-3;1);(-1;3);(3;-1)}
TH1: 2n+3-2k=1 và 2n+3+2k=-3
=>2n+3-2k+2n+3+2k=1-3
=>4n+6=-2
=>4n=-8
=>n=-2(nhận)
TH2: 2n+3-2k=-3 và 2n+3+2k=1
=>=>2n+3-2k+2n+3+2k=1-3
=>4n+6=-2
=>4n=-8
=>n=-2(nhận)
TH3: 2n+3-2k=-1 và 2n+3+2k=3
=>2n+3-2k+2n+3+2k=-1+3=2
=>4n+6=2
=>4n=-4
=>n=-1(nhận)
TH4: 2n+3-2k=3 và 2n+3+2k=-1
=>2n+3-2k+2n+3+2k=-1+3=2
=>4n+6=2
=>4n=-4
=>n=-1(nhận)
Đúng 0
Bình luận (0)
