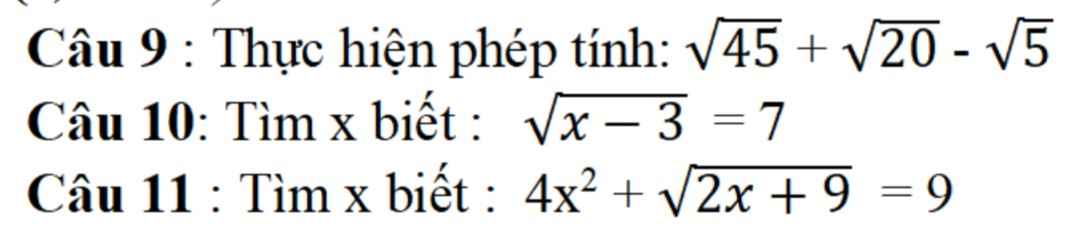\(9,=3\sqrt{5}+2\sqrt{5}-\sqrt{5}=4\sqrt{5}\\ 10,\Leftrightarrow x-3=49\Leftrightarrow x=52\\ 11,\Leftrightarrow\sqrt{2x+9}=9-4x^2\left(-\dfrac{3}{2}\le x\le\dfrac{3}{2}\right)\\ \Leftrightarrow2x+9=81-72x^2+16x^4\\ \Leftrightarrow16x^4-72x^2-2x+72=0\\ \Leftrightarrow\left(4x^2-2x-9\right)\left(2x^2+x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}4x^2-2x-9=0\\2x^2+x-4=0\end{matrix}\right.\\ \text{Kết hợp ĐKXĐ: }\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{37}}{4}\\x=\dfrac{-1+\sqrt{33}}{4}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Các câu hỏi tương tự

Giúp mình bài 3a vs 4 vs ạ

Giúp vs ạ! Mình sắp thi r ạ!!
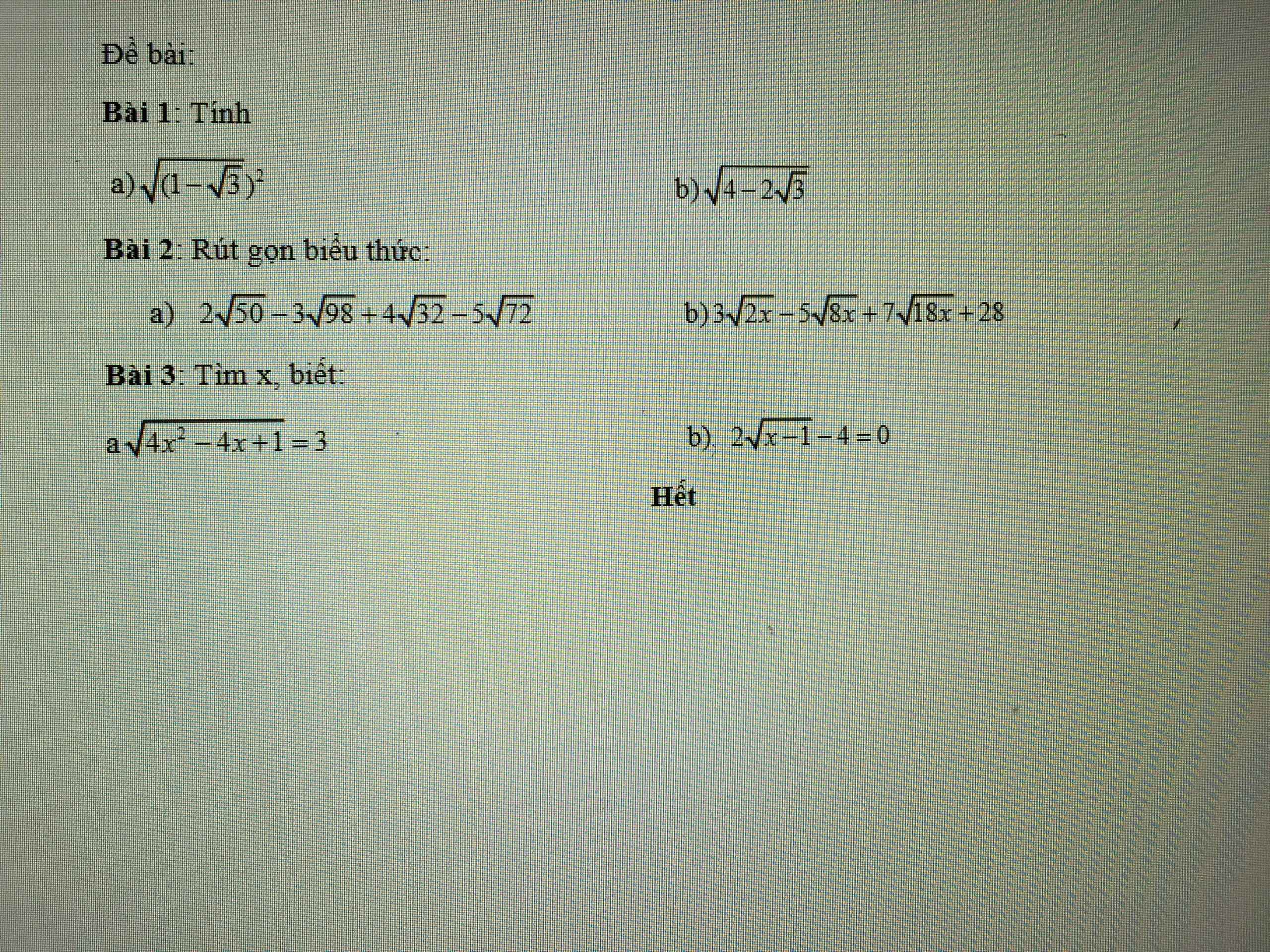 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!
Làm giúp mình bài này vs ạ làm giúp mình ý b và d thôi ạ 
giúp em vs ạ em cần gấp.cảm ơn ạ
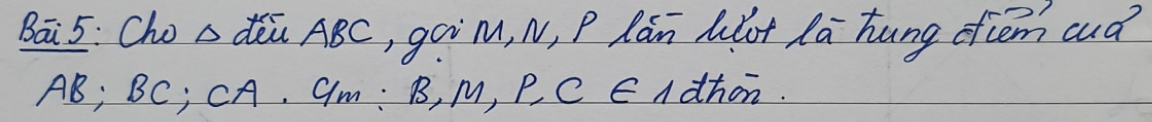
Giúp mk lm vs ạ
Câu 13-14 ạ
giúp vs ạ ! mk chỉ cần p2 thôi ạ !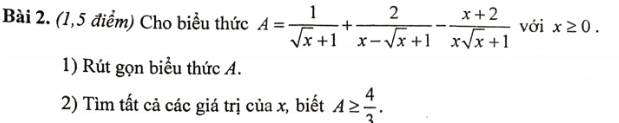
giúp mình lm câu b ý 2 vs câu c vs ạ. mình đg cần gấp ạ
Giúp vs ạ em đang cần gấp hôm nay ạ
giúp em vs ạ. 4h em phải nộp rùi ạ