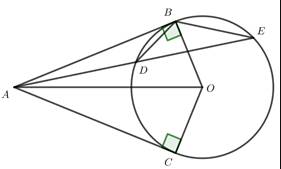
a.Vì AB và AC là tiếp tuyến cảu đường tròn (o) (gt)
=> AB\(\perp\)OB tại B và AC\(\perp\)OC tại C
=> ^ABO=90o và ^ACO=90o
Xét tứ giác ABOC có: ^ABO+^ACO=180o; mà 2 góc này ở vị trí đối nhau
=> Tứ giác ABOC nội tiếp
Vậy...
1: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
2: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại I và I là trung điểm của BC
Xét ΔOBA vuông tại B có BI là đường cao
nên \(IA\cdot IO=IB^2\)
3: ΔOED cân tại O
mà OH là đường cao
nên H là trung điểm của ED và OH là phân giác của góc EOD
Xét ΔOBA vuông tại B có BI là đường cao
nên \(OI\cdot OA=OB^2=R^2\)
Xét ΔOHA vuông tại H và ΔOIK vuông tại I có
\(\widehat{HOA}\) chung
Do đó: ΔOHA~ΔOIK
=>\(\dfrac{OH}{OI}=\dfrac{OA}{OK}\)
=>\(OH\cdot OK=OA\cdot OI\)
=>\(OH\cdot OK=R^2=OD^2\)
=>\(\dfrac{OH}{OD}=\dfrac{OD}{OK}\)
Xét ΔOHD và ΔODK có
\(\dfrac{OH}{OD}=\dfrac{OD}{OK}\)
\(\widehat{HOD}\) chung
Do đó: ΔOHD~ΔODK
=>\(\widehat{OHD}=\widehat{ODK}\)
=>\(\widehat{ODK}=90^0\)
Xét ΔODK và ΔOEK có
OD=OE
\(\widehat{DOK}=\widehat{EOK}\)
OK chung
Do đó: ΔODK=ΔOEK
=>\(\widehat{ODK}=\widehat{OEK}\)
=>\(\widehat{OEK}=90^0\)
Ta có: \(\widehat{KEO}=\widehat{KDO}=\widehat{KIO}=90^0\)
=>K,E,O,I,D cùng thuộc đường tròn đường kính KO