
giúp với chiều thi rồii
Câu 9 (2.0 điểm). Cho hình vuông \(ABCD\). Trên tia đối tia \(DA\) lấy điểm \(P\) sao cho \(DP = DA\). Gọi \(H\) chân đường vuông góc kẻ từ \(A\) đến \(BP\).
a) Chứng minh \(BC^2 = BH \cdot BP\) và \(\triangle BHC \sim \triangle BCP\).
b) Gọi \(M\) là trung điểm của \(HP\). Đường thẳng \(AM\) và \(BC\) cắt nhau tại điểm \(E\). Chứng minh \(EC \cdot EB = EM \cdot EA\).
a: Xét ΔBAP vuông tại A có AH là đường cao
nên \(BH\cdot BP=BA^2\)
=>\(BH\cdot BP=BC^2\)
=>\(\frac{BH}{BC}=\frac{BC}{BP}\)
Xét ΔBHC và ΔBCP có
\(\frac{BH}{BC}=\frac{BC}{BP}\)
góc HBC chung
Do đó: ΔBHC~ΔBCP











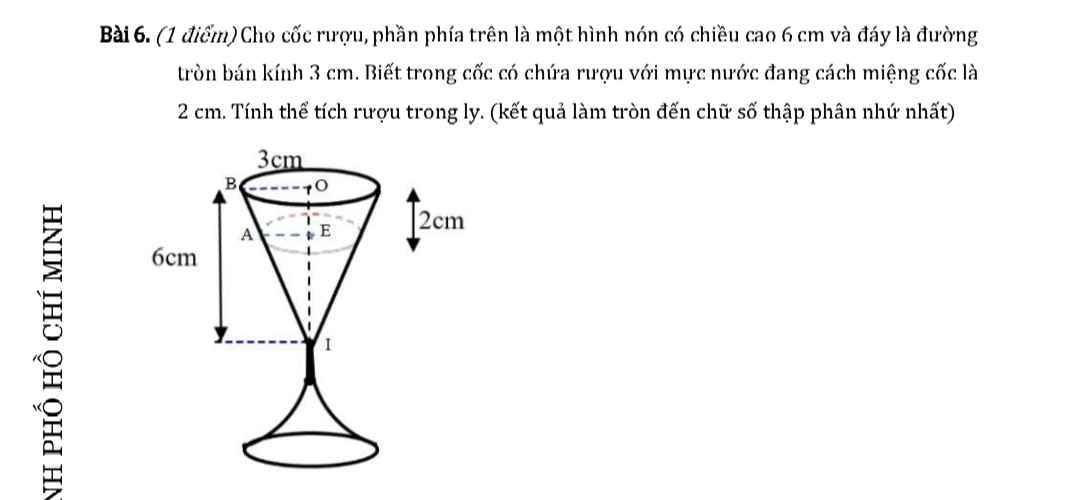




 giúp em với ạ, mai em thi rồi
giúp em với ạ, mai em thi rồi