\(a,\left(d\right)\text{//}\left(d'\right)\Leftrightarrow\left\{{}\begin{matrix}m+1=-m+8\\2m\ne-6\end{matrix}\right.\Leftrightarrow m=\dfrac{7}{2}\\ b,\Leftrightarrow\left\{{}\begin{matrix}m+2\ne-m+8\\2m=-6\end{matrix}\right.\Leftrightarrow m=-3\\ c,\text{Gọi điểm cố định mà }\left(d'\right)\text{ đi qua với mọi }m\ne8\text{ là }A\left(x_0;y_0\right)\\ \Leftrightarrow y_0=\left(8-m\right)x_0+2m\\ \Leftrightarrow mx_0-8x_0-2m+y_0=0\\ \Leftrightarrow m\left(x_0-2\right)+\left(y_0-8x_0\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-2=0\\y_0-8x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=16\end{matrix}\right.\\ \Leftrightarrow A\left(2;16\right)\\ \text{Vậy đt đi qua }A\left(2;16\right),\forall m\ne8\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Làm giúp mình câu a,b với ạ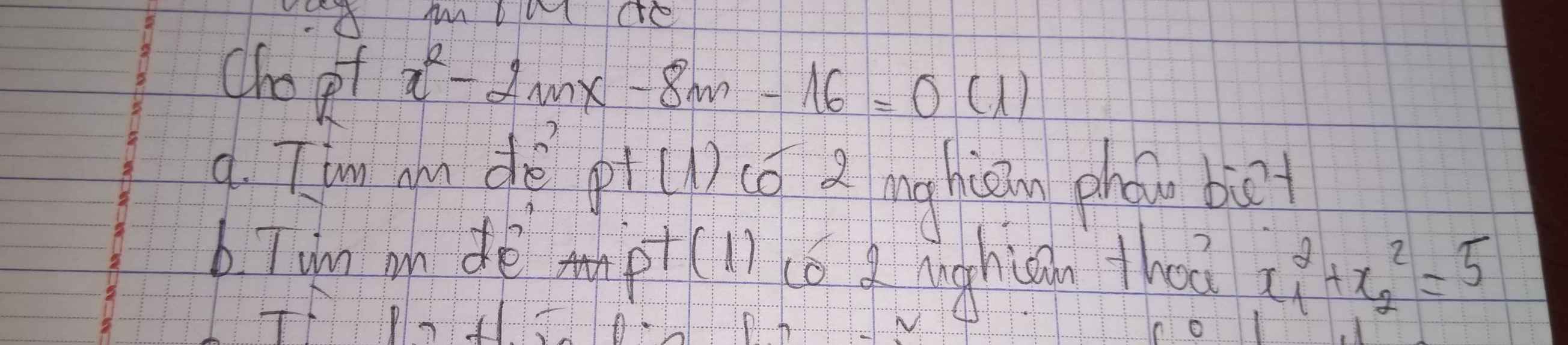
làm giúp e bài 4 câu b với ạ
mọi người giúp em câu b và câu c với ạ, câu (a) em làm được rồi.
Đọc tiếp
mọi người giúp em câu b và câu c với ạ, câu (a) em làm được rồi.
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
giúp e giải bài này với ạ
câu b c d thui nha mng

Làm cho em bài 3 với ạ , làm giúp em câu C thôi ạ.Em cảm ơn ạ 
Giúp em với ạ vẽ phụ em câu ạ nữa nha cảm ơn ạ
làm câu 8 và câu 9 giúp mình với ạ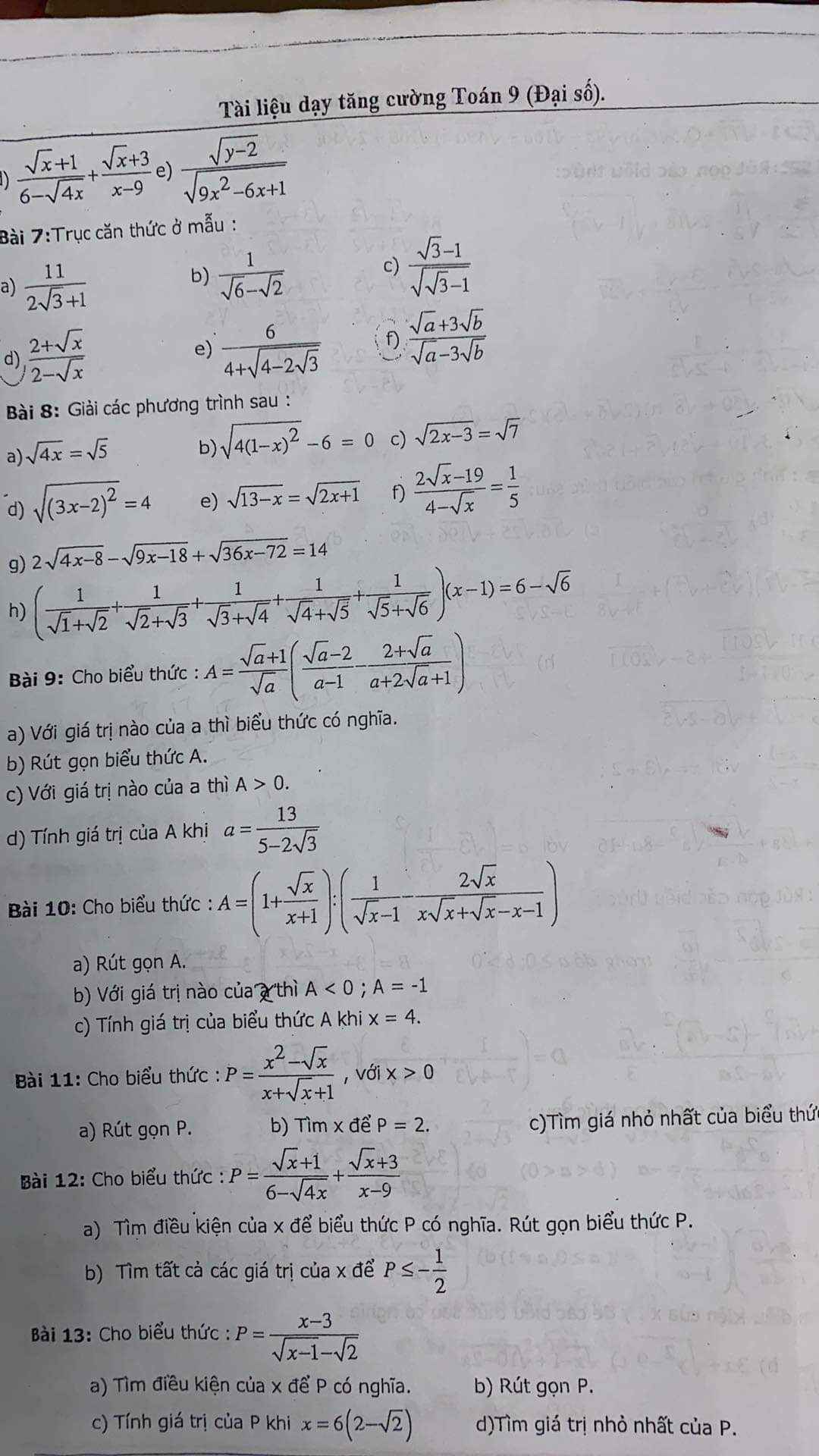

làm giúp mình câu 5 :câu 3 với!giải dõ hộ mình với ạ!













