Để bất phương trình \(\left(m+2\right)x^2-2\left(m+2\right)x+6< 0\) vô nghiệm
⇔ Δ'<0
⇔\(\left(m+2\right)^2-6\left(m+2\right)< 0\)
⇔\(m^2-2m-8< 0\)
⇒ \(\left\{{}\begin{matrix}-2< m< 4\\m\in Z\end{matrix}\right.\) ⇒ S=\(\left\{-1;0;1;2;3\right\}\)
⇒ Tổng các phần tử tập hợp S là:
-1+0+1+2+3=5
Đúng 2
Bình luận (0)
Các câu hỏi tương tự
2k4 trở lên đg on..
lên tiếng cho mình với..
mình có bài tập chưa giải ra đc..cần mn giúp!!
Giúp em giải bài giải bài này đc k ạ em đang cần gấp ạ !!!!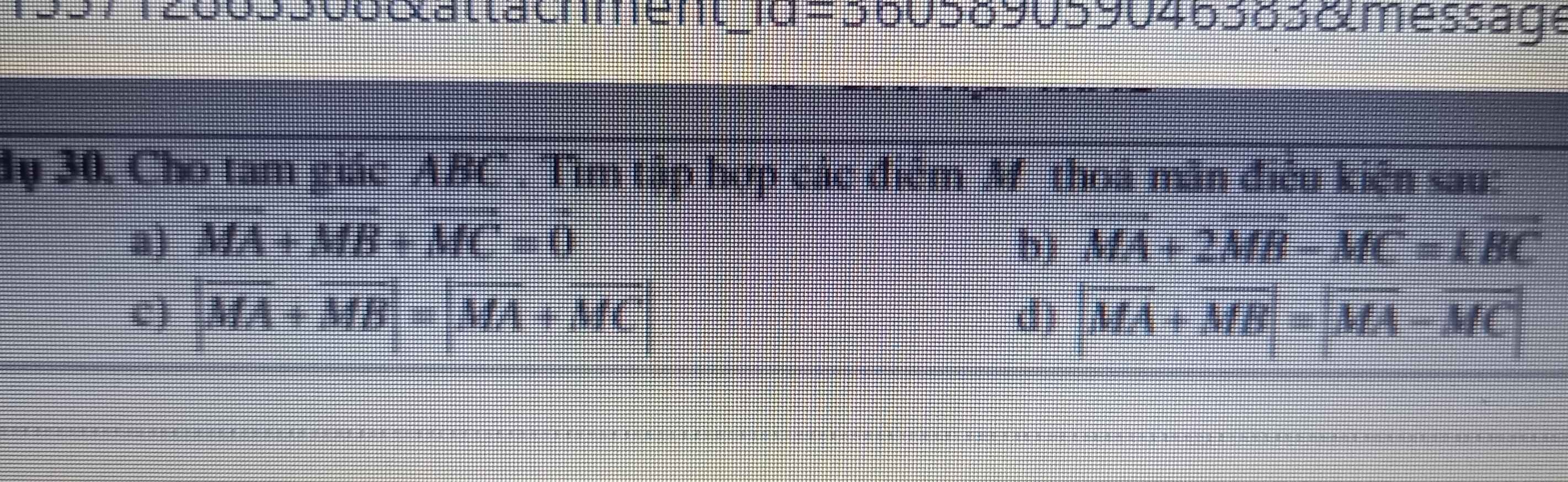
bộ bài 52 lá rút ra 2 lá. có bao nhiêu cách để 2 lá rút đc có tổng = 21
--------------
giúp tui với :((, mình khá cần để phục vụ cho thi học kì
Giải chi tiết giúp mình! Đừng tắt quá nha. Mn làm đc bài nào thì làm
Tìm a để hàm số xác định trên tập K đã chỉ ra:
a) \(y=\frac{2x+1}{x^2-6x+a+2}\) ; K=R
b) \(y=\sqrt{x-a}+\sqrt{2x-a-1}\) ; K=(0;+vô cực)
p/s: giúp 1 câu cũng đc :((
Bày mình 3 bài này với đc ko ạ
Mn giúp em với đc ko ak
Cho tam giác abc. Chứng minh rằng: tan\(\left(\dfrac{B+C}{2}\right)\)= cot\(\left(\dfrac{A}{2}\right)\)
mọi người giúp mình với ạ nếu đc có thể giải thích giúp mình luôn đc ko
Bài 1: A là nguyên tố mà nguyên tử có phân lớp ngoài cùng là 3p. B là nguyên tố mà nguyên tử cũng có phân lớp 3p, hai phân lớp này cách nhau 1 electron. B có 2 electron ở lớp ngoài cùng. A và B hơn kém nhau 1 lớp. Xác định số hiệu nguyên tử của A và BBài 2: Nguyên tố Clo có 2 đồng vị 35Cl và 37Cl . Khi cho 1,43g Zn tác dụng với lượng Clo dư thu được 2,992g muối khan ZnCl2. Hãy tính phần trăm số nguyên tử của mỗi loại đồng vị.Mong mn giúp với, mình vã lắm rồi!
Đọc tiếp
Bài 1: A là nguyên tố mà nguyên tử có phân lớp ngoài cùng là 3p. B là nguyên tố mà nguyên tử cũng có phân lớp 3p, hai phân lớp này cách nhau 1 electron. B có 2 electron ở lớp ngoài cùng. A và B hơn kém nhau 1 lớp. Xác định số hiệu nguyên tử của A và B
Bài 2: Nguyên tố Clo có 2 đồng vị 35Cl và 37Cl . Khi cho 1,43g Zn tác dụng với lượng Clo dư thu được 2,992g muối khan ZnCl2. Hãy tính phần trăm số nguyên tử của mỗi loại đồng vị.
Mong mn giúp với, mình vã lắm rồi!
Mn ơi cho em hỏi học kì 1 hs khá mà học kì 2 hs giỏi thì cả năm có được HSG ko ạ, với e cũng đag học lớp chọn nên có bị đuổi ko, mn giải đáp giúp em với😭















