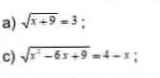`b)đk:x>=1`
`sqrt{x^2-2x+4}=x-1`
BP 2 vế ta có:
`x^2-2x+4=x^2-2x+1`
`<=>3=0` vô lý
Vậy pt vô nghiệm
`d)sqrt{x^2-2x+1}+sqrt{x^2-4x+4}=1`
`<=>sqrt{(x-1)^2}+sqrt{(x-2)^2}=1`
`<=>|x-1|+|x-2|=1`
`<=>|x-1|+|2-x|=1`
Áp dụng BĐT `|A|+|B|>=|A+B|`
`=>|x-1|+|2-x|>=|x-1+2-x|=1`
Dấu "=" xảy ra khi `(x-1)(2-x)>=0`
`<=>(x-1)(x-2)<=0`
`<=>1<=x<=2`
Vậy pt có nghiệm `S={x|1<=x<=2}`
Đúng 1
Bình luận (1)