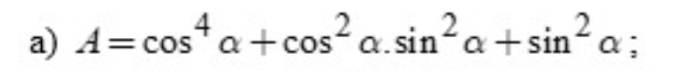Bài 6
a, bạn tự vẽ
b, Hoành độ giao điểm (P) ; (d) tm pt
\(\dfrac{1}{4}x^2+mx-2m-1=0\Leftrightarrow x^2+4mx-8m-4=0\)
\(\Delta'=4m^2-\left(-8m-4\right)=4m^2+8m+4=4\left(m+1\right)^2\)
Để (P) tiếp xúc (d) thì pt có nghiệm kép
-> 4(m+1)^2 = 0 <=> m = -1
c, Cho điểm cố định A có toạ độ A(x0;y0)
Thay vào (d) ta được \(y_0=mx_0-2m-1\Leftrightarrow\left(x_0-2\right)m-\left(1+y_0\right)=0\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=-1\end{matrix}\right.\)
Vậy (d) luôn đi qua điểm cố định A(2;1)
a) bạn tự vẽ nha
b) Phương trình hoành độ giao điểm :
\(-\dfrac{1}{4}x^2=mx-2m-1\)
<=> \(x^2+4mx-8m-4=0\)
\(\Delta=\left(4m\right)^2-4\left(-8m-4\right).1=16m^2+32m+16\)
d tiếp xúc (p) khi \(\Delta=16m^2+32m+16=16\left(m+1\right)^2=0\Leftrightarrow m=-1\)
c) Gọi điểm A(x1 ; y1)
Khi đó y1 = mx1 - 2m - 1
<=> mx1 - 2m - 1 - y1 = 0
<=> m(x1 - 2) + (-y1 - 1) = 0
<=> \(x_1=2;y_1=-1\)
=> thử vào (p) => -1 = 1/4 . (22) (đúng)
Vậy A(2 ; -1)

 giúp tui bài 6 với mng ơiiiiiii!
giúp tui bài 6 với mng ơiiiiiii!








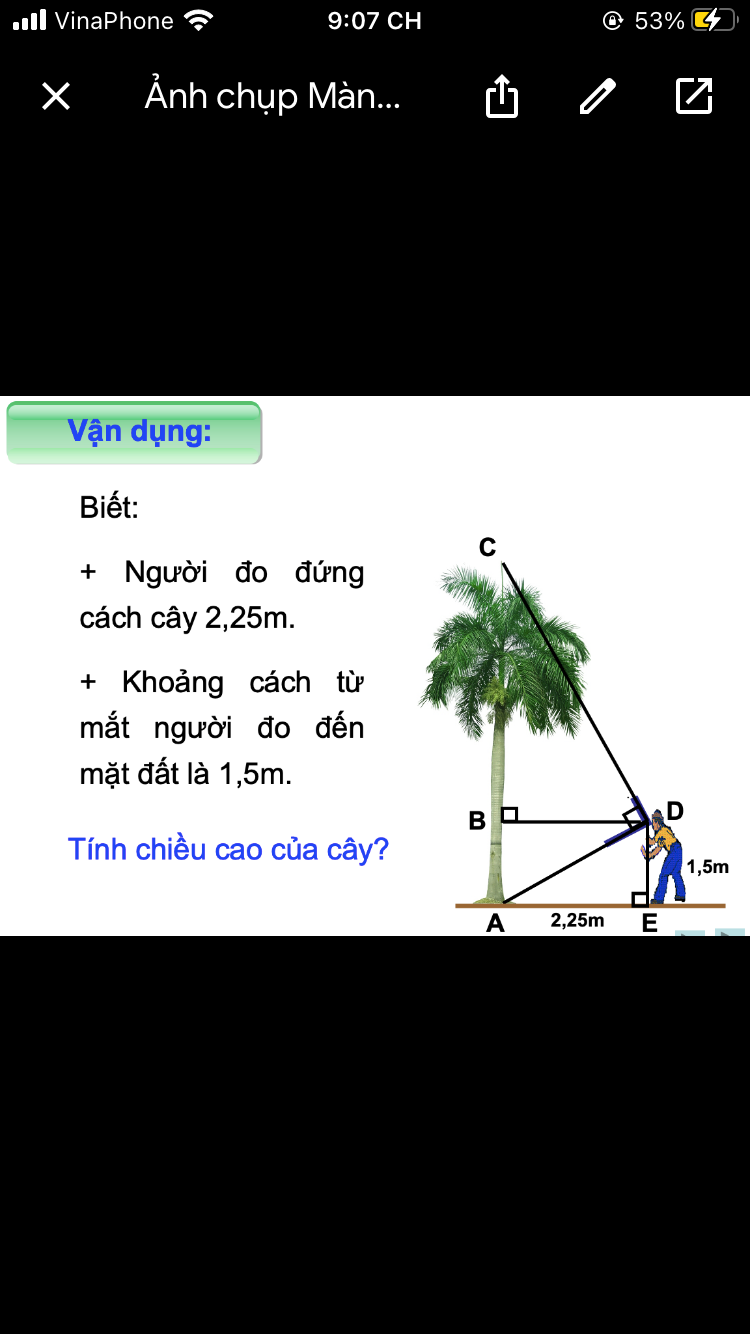

 mng giúp mình bài 9 với ạ
mng giúp mình bài 9 với ạ

 giúp tui bài 1 với :3
giúp tui bài 1 với :3