a: Ta có: \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2\)
\(=x^3-1-x^3+2\)
=1
b: ta có: \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5\)
\(=8x^3-y^3-8x^3-5\)
\(=-y^3-5\)
c: Ta có: \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2\)
\(=x^3+1-x^3+2\)
=3
d: Ta có: \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5\)
\(=8x^3+y^3-8x^3-5\)
\(=y^3-5\)
a) \(\left(x-1\right)\left(x^2+x+1\right)-x^3+2=x^3-1-x^3+2=1\)
b) \(\left(2x-y\right)\left(4x^2+2xy+y^2\right)-8x^3-5=8x^3-y^3-8x^3-5=-y^3-5\)
c) \(\left(x+1\right)\left(x^2-x+1\right)-x^3+2=x^2+1-x^3+2=3\)
d) \(\left(2x+y\right)\left(4x^2-2xy+y^2\right)-8x^3-5=8x^3+y^3-8x^3-5=y^3-5\)
e) \(\left(3x+2\right)\left(9x^2-6x+4\right)-27x^3-7=27x^3+8-27x^3-7=1\)
f) \(\left(3x-2\right)\left(9x^2+6x+4\right)-27x^3-7=27x^3-8-27x^3-7=-15\)














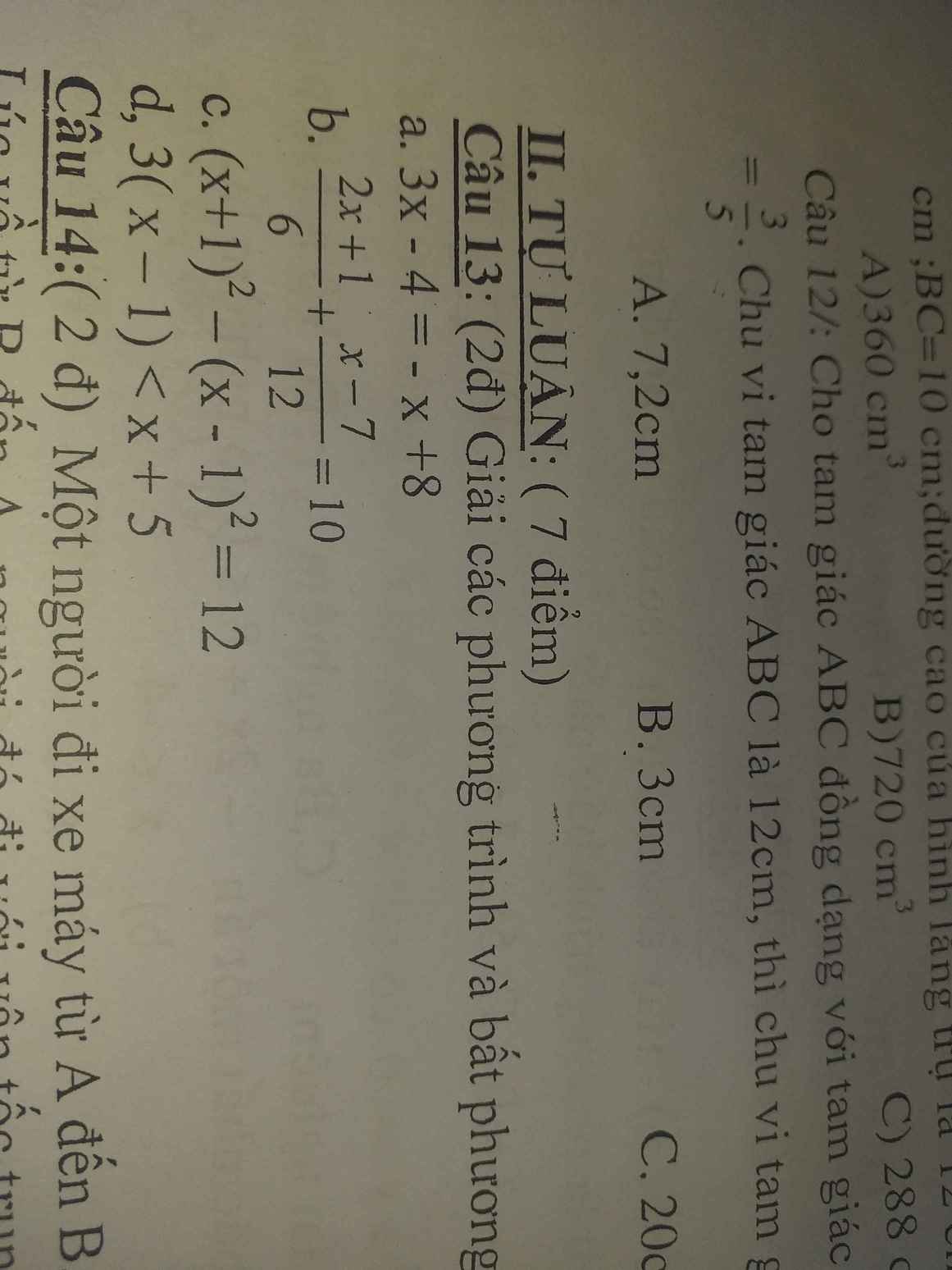


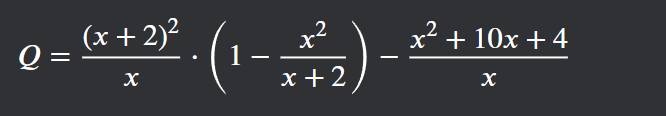

 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều

