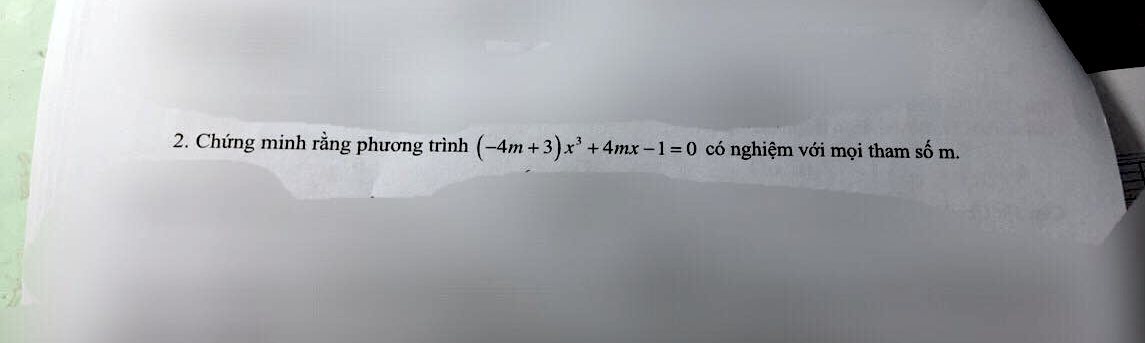Lời giải:
Xét hàm $f(x)=(-4m+3)x^3+4mx-1$ liên tục trên $R$
$f(1)=-4m+3+4m-1=2>0$
$f(-1)=4m-3-4m-1=-4<0$
$\Rightarrow f(1)f(-1)<0$
Do đó pt $f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(-1;1)$ với mọi $m$ (đpcm)
Đúng 1
Bình luận (0)