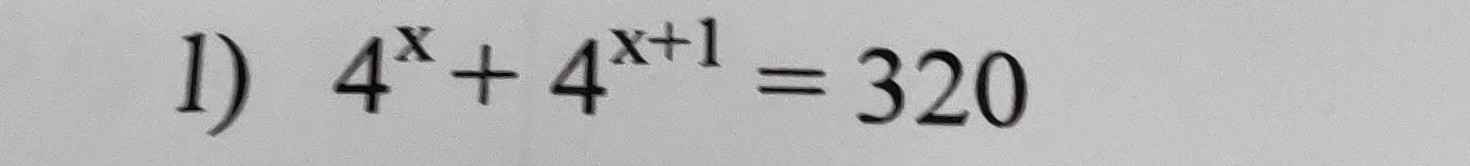Câu 1 :
\(...P=a^{\dfrac{1}{2}}.a^{\dfrac{1}{3}}.a^{\dfrac{1}{4}}=a^{\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}\right)}=a^{\dfrac{13}{12}}\)
Câu 2 :
a) \(log_39+log_330=log_3\left(9.30\right)=log_3270\)
b) \(log_575-log_53=log_5\dfrac{75}{3}=log_525=log_55^2=2\)
Câu 3 :
a) \(log_2\left(3x+1\right)=log_2\left(2x-4\right)\left(1\right)\)
\(Đk:\left\{{}\begin{matrix}3x+1>0\\2x-4>0\end{matrix}\right.\) \(\Leftrightarrow x>2\)
\(\left(1\right)\Leftrightarrow3x+1=2x-4\)
\(\Leftrightarrow x=-5\left(loại\right)\Leftrightarrow x\in\varnothing\)
b) \(log_{49}x=0,25\left(x>0\right)\)
\(\Leftrightarrow x=49^{0,25}=7^{2.0,25}=7^{0,5}=\sqrt{7}>0\left(nhận\right)\)