Đặt \(A=\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2048}\)
=>\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{11}}\)
=>\(2A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{10}}\)
=>\(2A-A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{10}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{11}}\)
=>\(A=1-\dfrac{1}{2^{11}}=\dfrac{2^{11}-1}{2^{11}}\)
\(\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{1}{12}-...-\dfrac{1}{6144}\)
\(=\dfrac{1}{3}-\dfrac{1}{3}\cdot A\)
\(=\dfrac{1}{3}-\dfrac{1}{3}\cdot\dfrac{2^{11}-1}{2^{11}}=\dfrac{2^{11}-2^{11}+1}{3\cdot2^{11}}=\dfrac{1}{3\cdot2^{11}}\)
Đặt \(A=\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2048}\)
=>\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{11}}\)
=>\(2A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{10}}\)
=>\(2A-A=1+\dfrac{1}{2}+...+\dfrac{1}{2^{10}}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{11}}\)
=>\(A=1-\dfrac{1}{2^{11}}=\dfrac{2^{11}-1}{2^{11}}\)
\(\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{1}{12}-...-\dfrac{1}{6144}\)
\(=\dfrac{1}{3}-\dfrac{1}{3}\cdot A\)
\(=\dfrac{1}{3}-\dfrac{1}{3}\cdot\dfrac{2^{11}-1}{2^{11}}=\dfrac{2^{11}-2^{11}+1}{3\cdot2^{11}}=\dfrac{1}{3\cdot2^{11}}\)
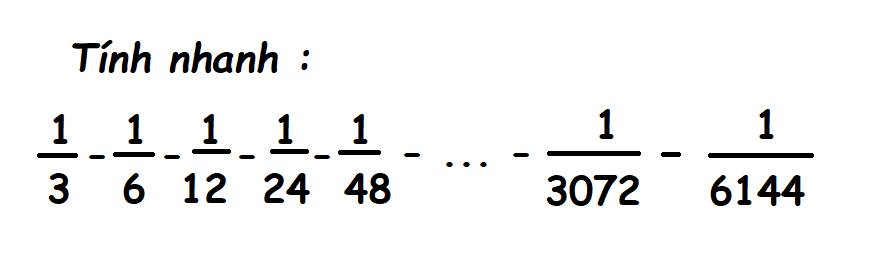
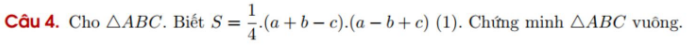
giúp mình với giải thích cho mình luôn nhé huhu mình cảm ơn
