\(#NgNgoc0409\)
Ta có: \(\dfrac{5z-3y}{4}=\dfrac{3x-4z}{5}=\dfrac{4y-5z}{3}\)
\(=>\dfrac{20z-12y}{16}=\dfrac{15x-20z}{25}=\dfrac{12y-15x}{9}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{20z-12y}{16}=\dfrac{15x-20z}{25}=\dfrac{12y-15x}{9}=\dfrac{20z-12y+15x-20z+12y-15x}{16+25+9}=0\)
\(=>\left\{{}\begin{matrix}\dfrac{20z-12y}{16}=0\\\dfrac{15x-20z}{25}=0\end{matrix}\right.\) \(\left(=\right)\left\{{}\begin{matrix}20z-12y=0\\15x-20z=0\end{matrix}\right.\) \(\left(=\right)\left\{{}\begin{matrix}20z=12y\\15x=20z\end{matrix}\right.\) \(\left(=\right)\left\{{}\begin{matrix}\dfrac{z}{3}=\dfrac{y}{5}\\\dfrac{x}{4}=\dfrac{z}{3}\end{matrix}\right.\)
\(=>\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{3}\)
\(=>x:y:z=4:5:3\left(dpcm\right)\)
giúp mình với mn ơi mình cần giúp khẩn cấp T_T
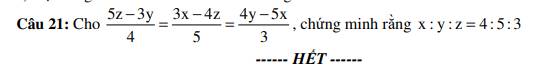
giúp mình với ạ,mình xin cảm ơn trước