f(1)=g(2)
=>\(2\cdot1^2+a\cdot1+4=1^2-5\cdot1-b\)
=>a+6=-b-4
=>a+b=-10(1)
f(-1)=g(5)
=>\(2\cdot\left(-1\right)^2+a\cdot\left(-1\right)+4=5^2-5\cdot5-b\)
=>2-a+4=-b
=>6-a=-b
=>-a+b=-6
=>a-b=6(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-10\\a-b=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=-4\\a-b=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-2\\b=a-6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-2\\b=-2-6=-8\end{matrix}\right.\)

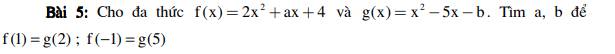





















 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước