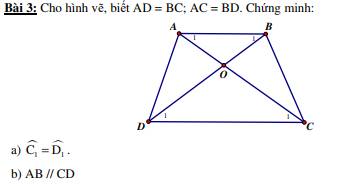
a: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó; ΔADC=ΔBCD
=>\(\widehat{ACD}=\widehat{BDC}\)
=>\(\widehat{C_1}=\widehat{D_1}\)
b: Gọi H là giao điểm của AD và BC
ΔADC=ΔBCD
=>\(\widehat{ADC}=\widehat{BCD}\)
=>\(\widehat{HDC}=\widehat{HCD}\)
Xét ΔHCD có \(\widehat{HCD}=\widehat{HDC}\)
nên ΔHCD cân tại H
=>HC=HD
HA+AD=HD
HB+BC=HC
mà AD=BC và HC=HD
nên HA=HB
Xét ΔHDC có \(\dfrac{HA}{HD}=\dfrac{HB}{HC}\)
nên AB//CD
Đúng 1
Bình luận (0)
giúp mình với mn ơi mình cần giúp khẩn cấp T_T
giúp mình với ạ,mình xin cảm ơn trước