Lời giải:
$A=\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{99}}$
$3A=1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{98}}$
$\Rightarrow 2A=3A-A=(1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{98}})-(\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{99}})$
$\Rightarrow 2A=1-\frac{1}{3^{99}}<1$
$\Rightarrow A< \frac{1}{2}$

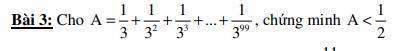




















 giúp mình với ạ,mình xin cảm ơn trước
giúp mình với ạ,mình xin cảm ơn trước