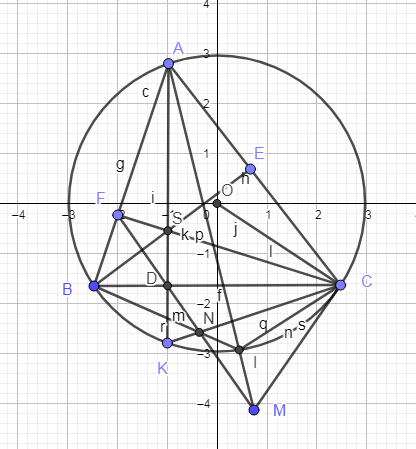
Giúp mình với mình đang cần gấp ạ . Bài 2 vẽ hộ mình hình nha 1) Một người quan sát ở đài hải đăng cao 150m so với mực nước biển nhìn thấy 1 chiếc thuyền ở xa với 1 góc nghiêng xuống là 25 độ. Hởi chiếc thuyền đang đứng cách chân hải đăng là bao nhiêu mét ( Nhớ gọi giúp mình nhé). 2) Cho tam giác ABC có 3 góc nhọn, AB<AC và nội tiếp (O). Ba đường cao AD,BE,CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K (với K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M. AM cắt đường tròn (O) tại I ( với I khác A). Kẻ MD cắt BI tại N. a) Cm tứ giác ACDF nội tiếp ( giải thích tại sao 2 góc vuông và ghi rõ DHNB tứ giác nội tiếp) b) Cm tam giác CMD cân tại M và ba điểm C,K,N thẳng hàng.
Bài 1:
Gọi CA là khoảng cách giữa chiếc thuyền và tháp hải đăng, BA là độ cao của tháp hải đăng
Theo đề, ta có: BA\(\perp\)CA tại A, BA=150m; \(\widehat{B}=25^0\)
Xét ΔBAC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AC=150\cdot tan25\simeq69,95\left(m\right)\)
Bài 2:
a: Xét tứ giác ACDF có \(\widehat{ADC}=\widehat{AFC}=90^0\)
nên ACDF là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{MCB}\) là góc tạo bởi tiếp tuyến MC và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{MCB}=\widehat{BAC}\)
mà \(\widehat{BAC}=\widehat{BDF}\left(=180^0-\widehat{FDC}\right)\)
và \(\widehat{BDF}=\widehat{MDC}\)(hai góc đối đỉnh)
nên \(\widehat{MDC}=\widehat{MCD}\)
=>ΔMCD cân tại M