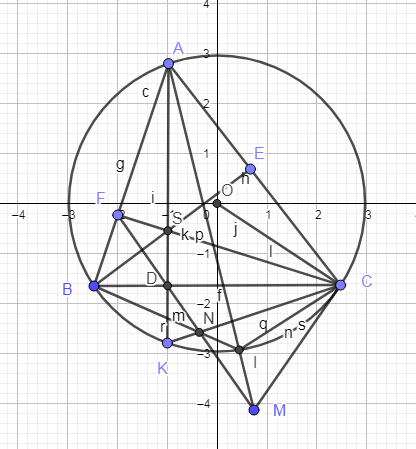
Cho tam giác ABC có 3 góc nhọn, AB < AC và nội tiếp đường tròn (O). Ba đường cao AD, BE, CF cắt nhau tại H. Tia AD cắt đường tròn (O) ở K( K khác A). Tiếp tuyến tại C của đường tròn (O) cắt đường thẳng FD tại M. AM cắt đường tròn (O) tại I( I khác A). MD cắt BI tại N. Chứng minh 3 điểm C, K, N thẳng hàng.
giúp gấp !!!!!!
ta có: \(MC^2=MI.MA\)
\(\Rightarrow MD^2=MI.MA\) ( do tam giác MCD cân tại M)
\(\Rightarrow\dfrac{MD}{MA}=\dfrac{ MI}{MD}\)
Xét tam giác MDI và tam giác MAD có :
\(\left\{{}\begin{matrix}DMAgócchung\\\dfrac{MD}{MA}=\dfrac{MI}{MD}\end{matrix}\right.\)
=> tam giác MDI đồng dạng tam giác MAD ( g -c)
=> góc MDI = góc MAD (1)
tứ giác DNIC nội tiếp => góc MDI = góc MCI (2)
từ 1 và 2 suy ra :góc NCI = góc HAD
mà góc MAD = góc KCI
=> góc NCI = góc KCI
vậy 3 điểm C ; K ; N thẳng hàng ( đpcm)