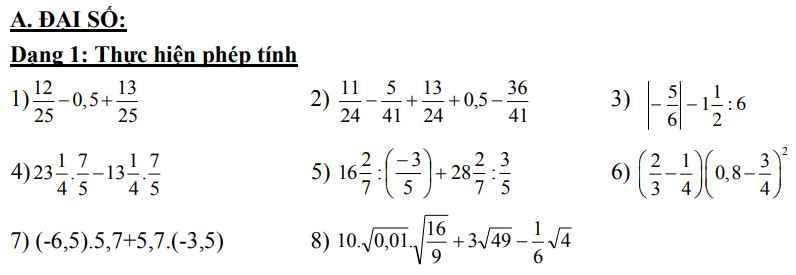Bài 3: Gọi số quyển sách lớp 7A;7B;7C quyên góp được lần lượt là a(quyển),b(quyển),c(quyển)
(Điều kiện: \(a,b,c\in Z^+\))
Số quyển sách tỉ lệ thuận với số học sinh
=>\(\dfrac{a}{35}=\dfrac{b}{45}=\dfrac{c}{40}\)
=>\(\dfrac{a}{7}=\dfrac{b}{9}=\dfrac{c}{8}\)
Lớp 7B và lớp 7C quyên góp được 255 quyển nên b+c=255
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{7}=\dfrac{b}{9}=\dfrac{c}{8}=\dfrac{b+c}{9+8}=\dfrac{255}{17}=15\)
=>\(a=15\cdot7=105\left(nhận\right)\)
vậy: Lớp 7A quyên góp được 105 quyển sách
Bài 4:
Gọi độ dài ban đầu của tấm vải thứ nhất, tấm vải thứ hai, tấm vải thứ ba lần lượt là a(m),b(m),c(m)
(Điều kiện: a>0; b>0; c>0)
Tổng độ dài ba tấm vải là 210m nên a+b+c=210
Sau khi bán đi 1/7 tấm vải thứ nhất; 2/11 tấm vải thứ hai và 1/3 tấm vải thứ ba thì độ dài còn lại của ba tấm vải bằng nhau nên ta có:
\(a\left(1-\dfrac{1}{7}\right)=b\left(1-\dfrac{2}{11}\right)=c\left(1-\dfrac{1}{3}\right)\)
=>\(\dfrac{6}{7}a=\dfrac{9}{11}b=\dfrac{2}{3}c\)
=>\(\dfrac{a}{\dfrac{7}{6}}=\dfrac{b}{\dfrac{11}{9}}=\dfrac{c}{\dfrac{3}{2}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{7}{6}}=\dfrac{b}{\dfrac{11}{9}}=\dfrac{c}{\dfrac{3}{2}}=\dfrac{a+b+c}{\dfrac{7}{6}+\dfrac{11}{9}+\dfrac{3}{2}}=\dfrac{210}{\dfrac{35}{9}}=54\)
=>\(\left\{{}\begin{matrix}a=54\cdot\dfrac{7}{6}=63\\b=54\cdot\dfrac{11}{9}=66\\c=54\cdot\dfrac{3}{2}=81\end{matrix}\right.\left(nhận\right)\)
Vậy: Độ dài ban đầu của ba tấm vải lần lượt là 63m; 66m; 81m
Bài 1:
a: y tỉ lệ thuận với x theo hệ số tỉ lệ là 1/3
=>\(y=\dfrac{1}{3}x\)
b:
| x | -12 | \(\dfrac{9}{2}\) | 1 | -12 | 0 | \(-\dfrac{1}{3}\) | 6 |
| y | -4 | \(\dfrac{3}{2}\) | \(\dfrac{1}{3}\) | -4 | 0 | \(-\dfrac{1}{9}\) | 2 |
Bài 2: x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
mà \(2x_1-3x_2=42,5;2y_1-3y_2=-8,5\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{2x_1-3x_2}{2y_1-3y_2}=\dfrac{42.5}{-8.5}=-5\)
=>\(y_1=-\dfrac{1}{5}\cdot x_1\)
=>\(y=-\dfrac{1}{5}x\)